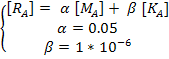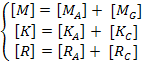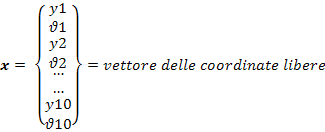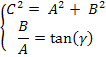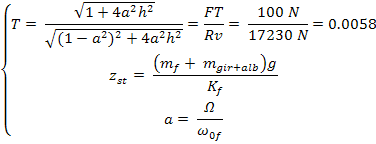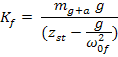Progetto monodimensionale di una pompa centrifuga multistadio
|
Traccia
Il progetto prevede di sviluppare i seguenti punti: · Schematizzazione a parametri concentrati della turbopompa: ipotesi e semplificazioni. · Scrittura matrici strutturali M, R, K · Calcolo modi di vibrare e frequenze proprie. Velocità critiche · [OPT] Sensibilità delle autosoluzioni al variare della finezza della schematizzazione · Definizione del forzamento dovuto ad eccentricità. · Risposta a regime: calcolare le funzione di risposta in frequenza degli spostamenti/rotazioni dei gdl della macchina. · [OPT] Sensibilità della risposta a regime al variare della velocità di rotazione della pompa · [OPT] Risposta a regime: calcolare le funzione di risposta in frequenza delle reazioni vincolari dei cuscinetti. · [OPT] Fondazione sospesa. Dimensionare una fondazione sospesa e valutare l’effetto sulle forze scaricate a terra.
Abbiamo svolto tutti i punti, compresi i punti facoltativi che sono contrassegnati da [OPT], con l’ausilio del programma di calcolo matriciale Matlab®. In allegato a questo progetto è presente il codice utilizzato con tutti i grafici generati( si veda l’ appendice A).
Schematizzazione a parametri concentrati della turbopompa: ipotesi e semplificazioni
Il sistema di cui studieremo le vibrazioni flessionali è costituito da un albero dal diametro costante (non sono stati considerati gli spallamenti e gli scavi per linguette) su cui sono calettate sette giranti; l’albero è vincolato allo statore (ritenuto infinitamente rigido) tramite tre cuscinetti, due dei quali sono posizionati alle estremità dell’albero mentre il terzo cuscinetto si trova a metà del tratto di albero che separa la quarta girante dalla quinta girante. Abbiamo ritenuto necessario inserire il terzo cuscinetto per via della elevata lunghezza dell’albero e per l’elevato numero di giranti presenti, fattori che avrebbero portato ad una elevata deformazione “statica” dell’albero. La seguente tabella riporta le principali caratteristiche dell’albero e delle giranti che sono stati dimensionati nella parte del corso di macchine di questo progetto:
Tabella 6: Dati di progetto
Il sistema è stato modellizzato come un sistema a parametri concentrati; di conseguenza sono state fatte le seguenti ipotesi e semplificazioni: · La massa dei cuscinetti è stata ritenuta trascurabile; · La deformabilità di ogni cuscinetto è stata modellizzata tramite un gruppo molla-smorzatore, di costante elastica Kc = 10^7 N/m e di smorzamento rc = 10^4 (N s)/m; · Ogni girante è stata considerata come un disco indeformabile dotato di massa m e momento di inerzia J che sono stati ricavati dal modello digitale 3-D del componente .
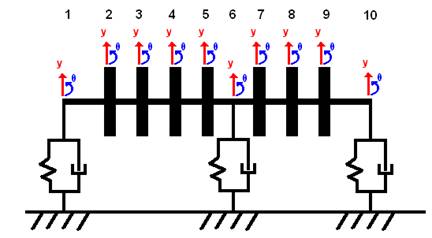
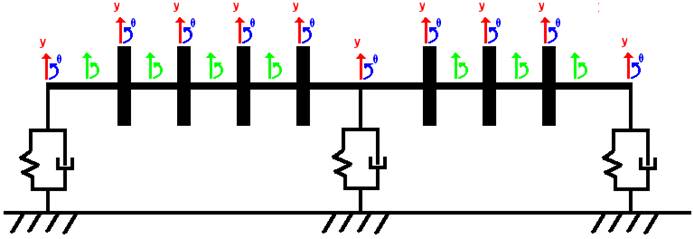
Sono stati inseriti 10 nodi lungo la struttura, in modo da avere un nodo in corrispondenza di ciascun cuscinetto e ciascuna girante. Poiché sono state studiate le vibrazioni flessionali nel piano, ad ogni nodo sono state associate una sola coordinata libera di traslazione (in direzione verticale, positiva se verso l’alto) ed una sola coordinata libera di rotazione ( attorno all’asse uscente dal foglio, positiva se in senso antiorario) per un totale di venti gradi di libertà:
Figura 9: schematizzazione a parametri concentrati della turbopompa
La distanza tra i cuscinetti situati alle estremità dell’albero e le rispettive prime giranti è pari al doppio del diametro dell’albero, mentre la distanza tra due giranti adiacenti è pari a 1.5 volte il diametro dell’albero; il terzo cuscinetto è posizionato a metà del segmento di albero che collega la quarta girante alla quinta girante, per cui si trova ad essere distante da esse 0.75 volte il diametro dell’albero.
Scrittura delle matrici strutturali M, R, K
Dato l’elevato numero di gradi di libertà presenti il calcolatore si è rivelato strumento indispensabile per la risoluzione delle diverse equazioni. Abbiamo utilizzato l’approcio matriciale per la scrittura dell’equazione di moto del sistema, in quanto si tratta di una forma matematica facilmente implementabile al calcolatore. In base alle ipotesi e alle semplificazioni descritte nel paragrafo precedente, all’albero sono associate una matrice di massa, una matrice di rigidezza e una matrice di smorzamento, ai cuscinetti sono associate una matrice di rigidezza ed una di smorzamento mentre alle giranti è associata solamente una matrice di massa. AlberoL’albero risulta suddiviso in nove segmenti: ogni segmento contiene quattro coordinate libere, due per ciascuno dei due nodi che lo delimitano. Per ogni segmento viene scritta una sottomatrice 4x4 di rigidezza, la cui struttura si ricava col metodo degli spostamenti, una sottomatrice 4x4 diagonale di massa ed una sottomatrice 4x4 di smorzamento. Riportiamo il codice della funzione di Matlab che genera le sottomatrici di massa e di rigidezza (nota: per la costruzione delle sottomatrici sono stati considerati i tratti di albero all’interno delle giranti):
function [mtx_m,mtx_k]=mtxfl(E,D,L,rho) % [mtx_m,mtx_k]=mtxfl(E,D,L,rho) % mtx_m=sottomatrice di massa % mtx_k=sottomatrice di rigidezza % E=modulo elastico acciaio = 193053.196e+6 Pa % D=diametro albero % L=lunghezza segmento % rho=densità materiale albero
Jn=pi/64*D^4; % momento di inerzia polare GEOMETRICO dell'albero m=pi/4*D^2*rho*L; % massa del tratto di albero J=Jn*rho*L; % momento di inerzia polare di massa
mtx_k = E*Jn * [ +12./L^3 6./L^2 -12./L^3 6./L^2; 6./L^2 +4./L -6./L^2 +2./L; -12./L^3 -6./L^2 +12./L^3 -6./L^2; 6./L^2 +2./L -6./L^2 +4./L];
mtx_m=diag([m J m J])/2;
Non è necessario calcolare le sottomatrici di smorzamento in quanto la matrice di smorzamento dell’albero si ricava come combinazione lineare delle matrici di massa e di rigidezza, poiché si suppone che le dissipazioni di energia siano dovute proprio alla massa ed alla deformabilità elastica del componente:
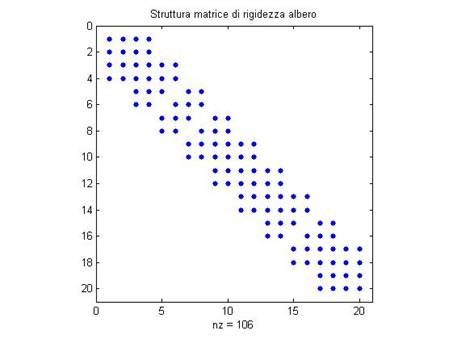
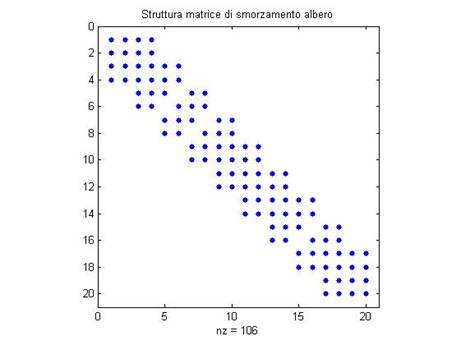
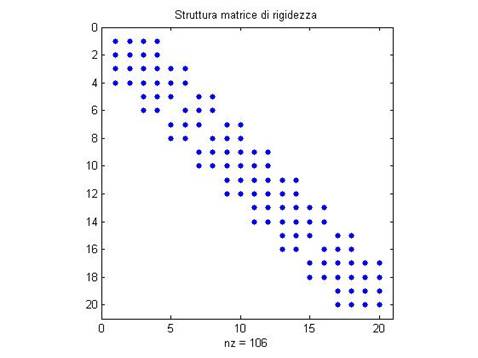
Le sottomatrici di massa e di rigidezza vanno unite a formare le matrici di massa e di rigidezza dell’albero, avendo cura di sommare i termini che si sovrappongono (si tratta dei termini associati ai nodi comuni a due segmenti adiacenti). Le matrici di rigidezza e di smorzamento dell’albero hanno quindi la seguente struttura:
Figura 10: struttura [K_a]
Figura 11: struttura [R_a]
GirantiLa struttura della matrice di massa associata alle giranti deriva dalla scrittura in forma matriciale dell’espressione dell’energia cinetica associata alle giranti:
La matrice Mg è di conseguenza una matrice diagonale con i termini sulla diagonale principali diversi da zero solo se associati ad una coordinata libera riferita ad una delle sette giranti. Per chiarire la struttura della matrice, riprendendo il codice utilizzato nello script di Matlab:
M_g = zeros(20,20); d=[0 0 m J m J m J m J 0 0 m J m J m J 0 0]; M_g = diag(d);
CuscinettiLa struttura delle matrici di rigidezza e di smorzamento derivano dalla scrittura in forma matriciale dell’energia potenziale elastica e della funziona dissipativa:
La matrice KC è di conseguenza una matrice diagonale i cui unici termini diversi da zero sono i termini di posto (1,1), (11,11) e (19,19) che sono in valore pari alla rigidezza dei cuscinetti. In modo analogo:
La matrice RC ha la stessa struttura della matrice KC ed i termini diversi da zero hanno valore pari allo smorzamento dei cuscinetti.
Matrici complessiveLe matrici di massa, rigidezza e smorzamento complessive del sistema sono così ricavate:
Queste matrici compongono l’equazione di moto del sistema nell’intorno della posizione di equilibrio statico:
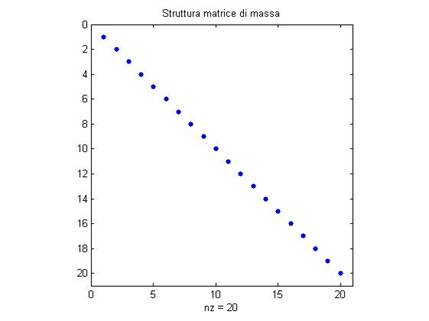
Figura 12: Struttura [M]
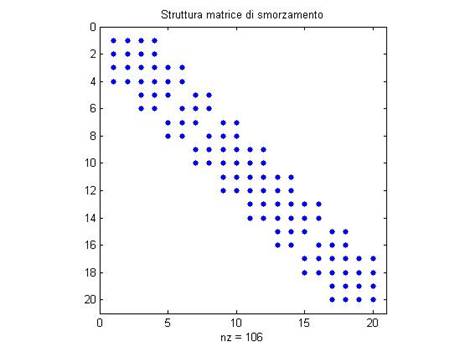
Figura 13: Struttura [R]
Figura 14: Struttura K
Modi di vibrare, frequenze proprie e velocità critiche
Per calcolare le frequenze proprie del sistema ed i modi di vibrare dello stesso ne abbiamo studiato il moto libero:
Cerchiamo delle soluzioni complesse dell’equazione differenziale del tipo:
Sostituendo nell’equazione differenziale la soluzione tipo e semplificando si ottiene la seguente equazione:
Si tratta di un problema agli autovalori (ω2) e agli autovettori ( X0 ) che è stato risolto grazie al comando Matlab eig(K,M) che implementa direttamente questo tipo di problema. Gli autovalori sono le pulsazioni proprie del sistema elevate al quadrato, per cui estraendone la radice e dividendole per 2π si ottengono le frequenze proprie del sistema.
Tabella 7: Frequenze proprie e velocità critiche
Le pulsazioni proprie del sistema ne costituiscono le velocità critiche di rotazione: se la pompa a regime ruota con velocità angolare pari ad una tra le velocità critiche il corrispondente grado di libertà si trova in risonanza e questo comporta spostamenti o rotazioni più elevate. La velocità massima di rotazione della pompa è limitata a 909 rad/s in quanto per motivi strutturali la velocità periferica allo scarico della girante non può superare i 100 m/s. Di conseguenza sono solo due le velocità critiche di interesse pratico: 560 rad\s (y1) e 860 rad\s (ϑ1). La velocità di rotazione nominale della pompa, Ω= 888 rad/s, è piuttosto vicina alla seconda velocità critica, tuttavia come si vedrà in seguito l’analisi della risposta a regime ha mostrato che il funzionamento della pompa non è compromesso da questo fatto.
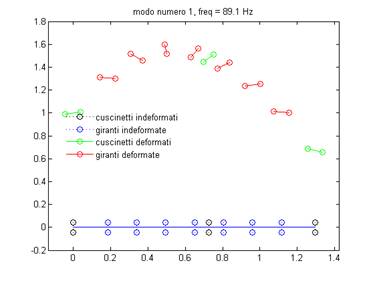
Gli autovettori costituiscono i modi di vibrare del sistema: l’i-esimo modo di vibrare è un vettore di venti elementi dove ciascun elemento rappresenta lo spostamento della corrispondente coordinata libera per uno spostamento unitario della i-esima coordinata libera quando la velocità di rotazione della pompa è pari alla i-esima velocità critica. Riportiamo solo alcuni dei modi di vibrare (tutti i modi di vibrare sono rappresentati graficamente nel report di Matlab allegato): Figura 15: Modo di vibrare n°1
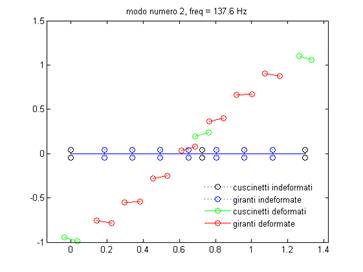
Figura 16: Modo di vibrare n°2
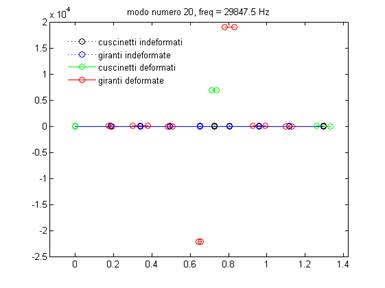
Figura 17: Modo di vibrare n°20
Analizzando i modi di vibrare si nota come gli spostamenti dei nodi nei modi di vibrare associati alle rotazioni sono più piccoli rispetto agli spostamenti dei nodi nei modi di vibrare associati alle traslazioni. E’ curioso osservare che per i modi di vibrare n° 17, 19 e 20 si ottengono dei valori per gli spostamenti dei nodi dell’ordine di 104 m.
Sensibilità delle autosoluzioni al variare della finezza della schematizzazione
Al fine di valutare la sensibilità delle autosoluzioni al variare della finezza della schematizzazione sono stati considerati due varianti del sistema originario: nella prima variante (sistema S1) è stato mantenuto costante il numero di coordinate libere ma non sono stati considerati nel calcolo delle sottomatrici strutturali dell’albero i tratti di albero all’interno delle giranti mentre nella seconda variante (sistema S2) è stato aumentato il numero di coordinate libere inserendo un nodo a metà dei tratti di albero compresi tra due giranti e tra una girante ed un cuscinetto. Lo schema seguente riporta il sistema utilizzato per la seconda variante, con in verde i nuovi gradi di libertà inseriti:
Figura 18: Sistema S2 a 34 gdl
Le procedure di calcolo utilizzate per trovare le velocità critiche, le frequenze proprie ed i modi di vibrare sono identiche alle procedure descritte nei paragrafi precedenti, per cui riportiamo solo i seguenti risultati:
Tabella 8: Confronto tra le velocità critiche
Dalla tabella notiamo che le velocità critiche subiscono delle modeste variazioni non considerando i tratti di albero all’interno delle giranti, mentre le variazioni sono molto più grandi aumentando il numero di gradi di libertà (e quindi la finezza della schematizzazione). In definitiva possiamo assumere che le velocità critiche sono sensibili alla finezza della schematizzazione,poco sensibili alla lunghezza dei segmenti di albero.
Per quanto riguarda i modi di vibrare:
Tabella 9: Confronto tra i modi di vibrare
Dalla tabella è evidente che i modi di vibrare sono molto sensibili sia alla finezza della schematizzazione sia alla lunghezza dei segmenti di albero. Definizione del forzamento dovuto ad eccentricità
Per effetto dello squilibramento delle giranti, sul sistema agiscono sette forzanti periodiche con andamento sinusoidale la cui espressione analitica si ottiene proiettando il modulo della forza di inerzia agente sul baricentro delle giranti sulla direzione verticale. Il modulo della forza di inerzia è direttamente proporzionale alla massa della girante, alla eccentricità e al quadrato della velocità angolare di rotazione della pompa:
“e” è l’eccentricità, ovvero la distanza tra il baricentro della girante e il centro di rotazione della stessa, mentre β è l’angolo di sfasamento della forzante. Abbiamo inserito dei valori arbitrari sia per le eccentricità (nell’ordine di pochi millimetri) sia per gli sfasamenti:
Tabella 10: Eccentricità, sfasamenti e modulo delle forzanti
Per inserire il forzamento nell’equazione di moto, ogni forzante è stata scritta nel seguente modo:
F0 è un numero complesso il cui modulo è pari al modulo della forzante ed il cui argomento è pari allo sfasamento della forzante. Le forzanti sono state unite a formare un vettore 20x1 denominato Q0 che contiene le componenti lagrangiane delle forze applicate al sistema. Risposta a regime: calcolo della funzione di risposta in frequenza
Con il termine “funzione di risposta in frequenza” si intende la funzione di trasferimento H del sistema vibrante sottoposto a forzamento periodico armonico calcolata per diversi valori della velocità di rotazione della pompa. La funzione di trasferimento è una matrice 20x20 il cui generico termine Hij rappresenta la risposta dell’i-esimo grado di libertà al forzamento unitario del j-esimo grado di libertà. Ogni termine della funzione di trasferimento è un numero complesso che pertanto è dotato di modulo e di un argomento che rappresentano rispettivamente il modulo della risposta del sistema e la fase della risposta.
Per ricavare la funzione di trasferimento basta sostituire nell’equazione di moto la soluzione tipo X= X0 eiωt e una volta raccolto e semplificato il termine eiωt basta dividere tutto per F0 :
Abbiamo calcolato la funzione di trasferimento per dei valori della velocità angolare compresi tra 1 e 10000 rad/s anche se in realtà non è possibile far funzionare la pompa a velocità superiori ai 909 rad/s, ma ciò ci ha consentito di meglio evidenziare l’andamento dei termini della funzione di trasferimento in funzione della velocità di rotazione della pompa.
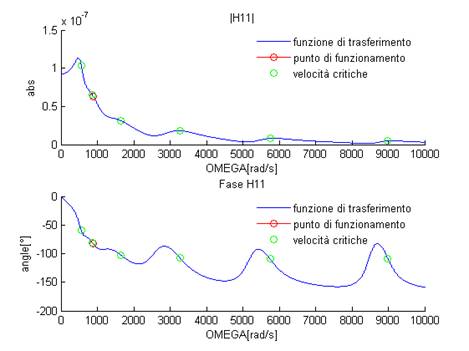
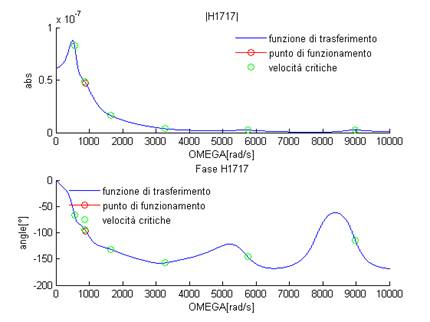
Riportiamo solo alcuni dei grafici delle funzioni di trasferimento dei vari gradi di libertà; gli altri grafici realizzati sono visualizzabili nel report di Matlab in allegato (vedi appendice A). In tutti i grafici si nota come la risonanza del primo grado di libertà (y1) produce gli effetti maggiori sulla risposta dei vari gradi di libertà del sistema. Le risonanze degli altri gradi di libertà producono invece effetti più contenuti. Figura 19: H11
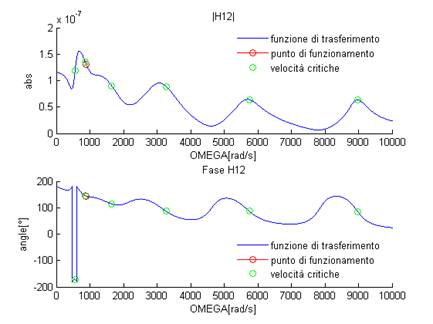
Figura 20: H12
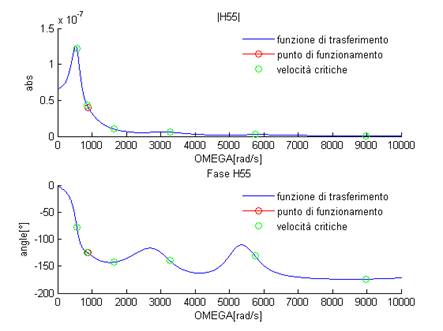
Figura 21: H55
Figura 22: H1717
Sensibilità della risposta a regime al variare della velocità di rotazione della pompa
In questo paragrafo l’obiettivo che ci siamo posti è di verificare se per piccole variazioni della velocità di funzionamento della pompa (variazioni che possono essere dovute a fattori di disturbo esterni e che sono comuni nel funzionamento reale della turbomacchina) la risposta a regime dei vari gradi di libertà subisce grandi variazioni e se queste variazioni possono rappresentare un pericolo per il corretto funzionamento della pompa. Riprendendo il procedimento utilizzato nel paragrafo precedente per il calcolo della funzione di trasferimento, sostituiamo nell’equazione di moto la soluzione tipo e risolvendo il seguente sistema lineare è possibile ricavare il modulo e la fase della riposta a regime dei gradi di libertà:
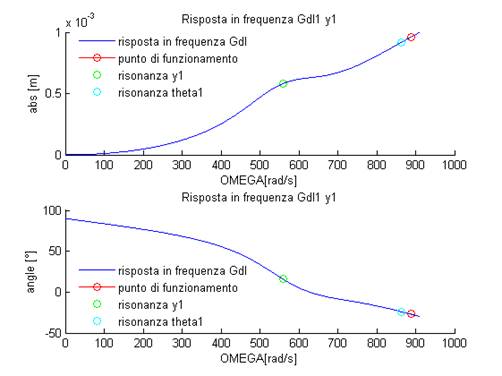
Figura 23: Riposta in frequenza di y1
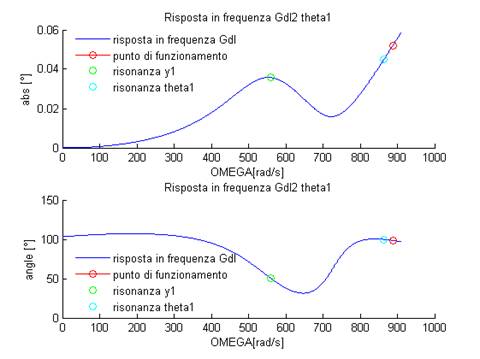
Figura 24: Riposta in frequenza di theta1
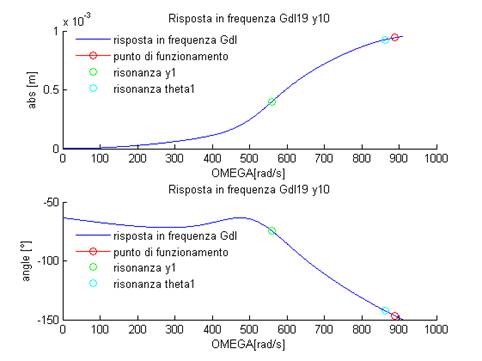
Figura 25: Riposta in frequenza di y10
Come sempre l’elenco completo di tutte le riposte in frequenza dei gradi di libertà è presente nel report di Matlab allegato. Dai grafici è evidente che il punto di funzionamento si trova vicino alla velocità critica del secondo grado di libertà (ϑ1) ma ciò non genera alcun problema per il funzionamento della pompa, in quanto l’ampiezza di moto a regime di tutti i gradi di libertà si mantiene al di sotto del millimetro per le traslazione e di 0.1° per le rotazioni, valori molto piccoli di spostamento che non dovrebbero creare problemi per i collegamenti tra la pompa e il circuito idraulico. La seguente tabella mostra le ampiezze di moto a regime dei vari gradi di libertà per il punto di funzionamento, per la velocità massima di rotazione della pompa e per la velocità di risonanza del secondo grado di libertà ( [m] per i gradi di libertà delle traslazioni, [°] per i gradi di libertà di traslazione).
Tabella 11: Risposta a regime per diverse velocità di funzionamento
Funzioni di risposta in frequenza delle reazioni vincolari dei cuscinetti
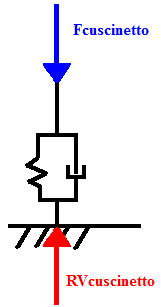
Le reazioni vincolari sono state ricavate imponendo l’equilibrio delle forze agenti sul cuscinetto, secondo il disegno seguente:
Ne consegue che le reazioni vincolari sono uguali in modulo alle forze agenti sul cuscinetto, ma hanno verso opposto. Sfruttando le risposte a regime dei gradi di libertà di traslazione verticale associati ai cuscinetti (y1, y11, y19) per 1<Ω<909 rad/s è si ricavano le risposte in frequenza delle reazioni vincolari dei cuscinetti. Per la generica reazione vincolare RV:
La somma di queste due funzioni armoniche è ancora una funzione armonica di cui vogliamo ricavarne modulo e fase; cerchiamo di scrivere la somma di queste due funzioni come:
Utilizzando la formula di addizione del seno e confrontando l’espressione che si ottiene con l’espressione originaria della reazione vincolare si ottiene il seguente sistema di condizioni:
Risolvendo questo sistema di due equazioni in due incognite è possibile trovare il modulo e la fase della generica reazione vincolare per ogni valore di Ω. Tornando alla forma complessa:
Dove
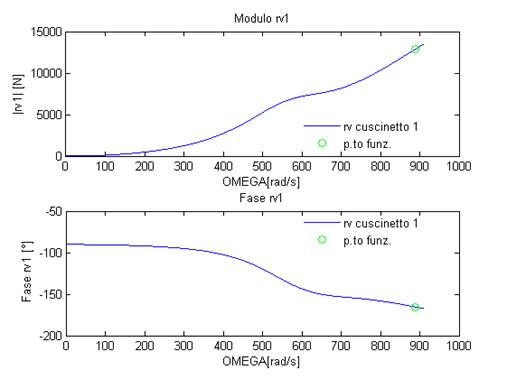
Le reazioni vincolari dei 3 cuscinetti, in funzione della velocità di rotazione della pompa, hanno il seguente andamento: Figura 26: Risposta in frequenza Rv1
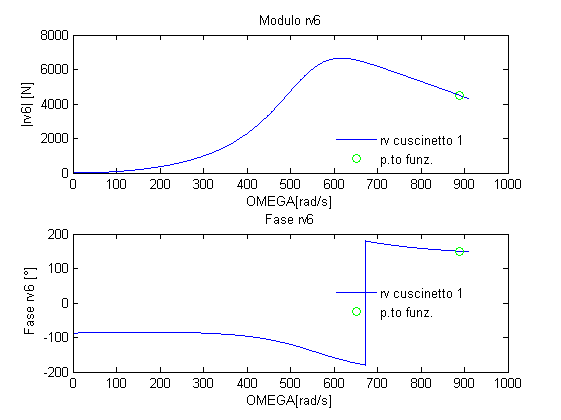
Figura 27: Risposta in frequenza Rv6
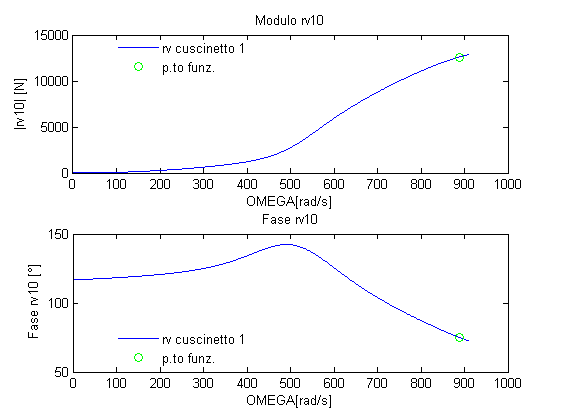
Figura 28: Risposta in frequenza Rv10
E’ curioso osservare che, mentre il modulo delle reazioni vincolari agenti sul primo nodo e sul decimo nodo aumentano all’aumentare della velocità di rotazione della pompa, il modulo della reazione vincolare agente sul sesto nodo (terzo cuscinetto) diminuisce all’aumentare della velocità di rotazione della pompa. Tabella 12: Modulo delle reazioni vincolari per diverse velocità di funzionamento
Complessivamente la forza trasmessa a terra è pari alla somma delle reazioni vincolari dei 3 cuscinetti e per ricavarne modulo e fase abbiamo utilizzato il formalismo complesso:
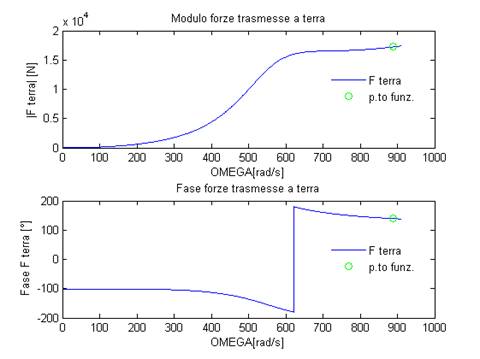
Si noti la semplicità del formalismo complesso, che permette di ragionare nel dominio delle frequenze: per sommare tre funzioni armoniche di diverso modulo e diversa fase è stato solo necessario sommare tre numeri complessi, mentre se si ragiona nel dominio del tempo come è stato fatto per il calcolo delle singole reazioni vincolari è necessario utilizzare diverse formule trigonometriche, risolvere sistemi ecc a tutto discapito della semplicità di implementazione del problema al calcolatore. Figura 29: Risposta in frequenza forze trasmesse a terra
Osserviamo che la forza trasmessa a terra è pressoché costante nell’intorno del punto di funzionamento. Dimensionamento di una fondazione sospesa
Per il dimensionamento della fondazione sospesa occorre studiare il moto di un semplice sistema ad un grado di libertà sottoposto al forzamento periodico delle reazioni vincolari dei cuscinetti. Sono presenti tre incognite: massa, smorzamento e rigidezza della fondazione. Abbiamo scelto di imporre che la fondazione soddisfi il seguente requisito inerente la forza trasmessa a terra:
Per un sistema vibrante ad un grado di libertà sottoposto a forzamento è possibile scrivere il seguente sistema di equazioni (T è la trasmissibilità della fondazione, cioè il rapporto tra la forza trasmessa a terra e la forza agente sulla fondazione stessa):
E’ possibile ricavare il valore della pulsazione adimensionale (a) dalla prima equazione; occorre risolvere una equazione biquadratica:
Il discriminante dell’equazione è positivo per qualsiasi valore di h>0, per cui abbiamo scelto un valore per lo smorzamento adimensionale pari all’1 %:
Un valore del 1 % per lo smorzamento adimensionale h è comunemente utilizzato per la realizzazione di fondazioni in cemento armato.
Dalla definizione di pulsazione adimensionale (a) si esprime la massa della fondazione in funzione della rigidezza della stessa:
Sostituendo questa espressione nell’equazione dell’affondamento statico è possibile ricavare la rigidezza della fondazione:
Poiché la rigidezza è un numero positivo, si è trovata una condizione sull’affondamento statico minimo della fondazione:
Abbiamo scelto di imporre un affondamento statico di 0.003 m, cioè di 3 mm, valore modesto che non dovrebbe creare problemi di collegamento della pompa al circuito.
Calcoliamo l’ampiezza di moto a regime della fondazione:
Osserviamo che con l’utilizzo della fondazione sospesa le forze trasmesse a terra sono state ridotte a 100 N a partire dai 17230 N trasmessi a terra senza l’utilizzo della fondazione.
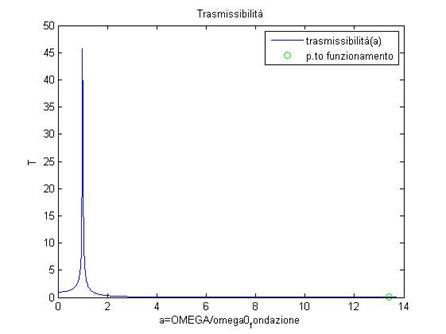
Figura 30: Andamento della trasmissibilità in funzione della pulsazione adimensionale
La figura evidenzia come la fondazione lavora nel campo della fondazione sospesa: il rapporto tra la forza trasmessa a terra e la forza che agisce sulla fondazione è molto minore dell’unità. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||