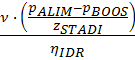PARTE B

 

Procediamo ora con il dimensionamento del sistema. In particolare ci concentreremo nel definire:

·         Triangoli di velocità all’ingresso e all’uscita della girante;

·         Angolo di scarico delle pale;

·         Diametri alla base e all’apice della pala per la sezione di ingresso;

·         Altezza di pala allo scarico;

·         Numero delle pale;

·         Diametro e velocità assoluta allo scarico del diffusore, che si suppone non palettato.

 

Per dimensionare il diametro dell’albero utilizziamo il criterio di Guest-Tresca che dice:

τ_MAX ≤ τ_AMM = 

Per trovare il diametro dell’albero dalla formula di τ_MAX, calcoliamo il valore del momento torcente con la seguente formula:

M_t =  =   à  M_t,MAX = 1.5 M_t

(il coefficiente 1,5 sta ad indicare il fattore di sicurezza)

Sapendo che

 =  = 0.97

E che

τ_MAX  =   

Sostituendo a τ_MAX  il valore di    e invertendo la formula, il diametro dell’albero risulta 0.0824 m.

Dal catalogo dei diametri commerciali prendiamo il diametro più vicino a quello trovato arrotondato per eccesso, in modo da sovradimensionare il sistema. Il diametro scelto è pari a 85 mm. Il diametro del mozzo deriva direttamente dal diametro dell’albero dalla relazione D_MOZZO=1.2D_ALBERO =102 mm .

 

Andiamo ora ad analizzare i triangoli delle velocità all’ingresso della girante con le ipotesi seguenti:

·         D_1,APICE tale che W_1,APICE sia minimizzata;

·         V_1,ASSIALE , quindi V_1t = 0;

·         V₁costante al variare del raggio.

 

Quindi dalle ipotesi possiamo assumere che V_1a = W_1a =costante(r)

 

Sapendo che V_1t=U+W_1t =0 allora:

W_1t= -U.

W_1a,APICE = V_1a = 

A₁= π/4  (D²_1,APICE – D²_1,BASE) – ingombro pale.

Dove l’ingombro delle pale è uguale a  z .

S , lo spessore delle pale, è noto ed è 2,5 mm, mentre z è il numero di pale ed è dato da:

z = 10 + 0.03D₂ = 17   arrotondato all’intero più vicino.

La velocità relativa all’ingresso della girante all’apice viene calcolata con la formula:

|W_1APICE| =

Dove W_1t,APICE = U =   = -444.12  D_1a

Attraverso il risolutore di Excel abbiamo ricavato il valore di D_1APICE dalla formula di W_1a,APICE minimizzando la funzione, come da ipotesi. I vincoli imposti per il risolutore sono quelli di costruzione, ovvero il rapporto fra D_1APICE e D_1BASE  minore di 0.7 e il rapporto tra D_1APICE e il diametro della girante D₂ compreso tra 0.5 e 0.7.

Tramite questa operazione siamo giunti al valore del diametro all’apice di 0.148 m minimizzando la velocità relativa W_1APICE al valore di 69.074 m/s. Tramite il valore di D_1a abbiamo ricavato la velocità W_1a,APICE che risulta pari a 21.47 m/s.

Per quanto riguarda i triangoli delle velocità abbiamo preso in considerazione il diametro medio della girante e di conseguenza i valori medi di tutte le velocità.

 

·         Triangolo delle velocita’ in ingresso

D_1MEDIO =  = 0.125 m

Dal diametro medio possiamo ricavare la velocità media di rotazione delle pale, ovvero la velocità di trascinamento

U =  = 55.47 m/s

Le velocità relative risultano:

W_1a,MEDIA = W1a = 21.47 m/s

W_1t,MEDIA =  U_1MED =  55.47 m/s

Quindi 

|W_1MEDIO |= 59.48 m/s

Gli angoli all’ingresso li abbiamo calcolati nella seguente maniera:

 

·         Triangolo delle velocita’ in uscita

Partiamo dal lavoro euleriano che nel nostro caso è uguale a U₂V_2t visto che V_1t = 0.

Sapendo che il lavoro euleriano si può scrivere anche come  ed è pari a 5677.57 J/kg; eguagliando le due espressioni ci ricaviamo il valore di V_2t: ciò che otteniamo è V_2t = 58.11 m/s.

W_2t la possiamo ricavare sommando vettorialmente i moduli di V_2t e U₂:

W_2t = V_2t-U₂ =  39.59 m/s

Per poter calcolare dobbiamo prima trovare il valore della componente della velocità relativa radiale all’uscita della girante.

Utilizziamo il rapporto di De Haller:

 che vale 0.85  à |W₂| = 0.85  |W_1MEDIO| = 50.59 m/s

Quindi               W_2r =  = 31.5 m/s

 

 

 

 

Ora possiamo passare a calcolare l’angolo adiacente alla velocità relativa in uscita:

W_2r = V_2r

V_2t=58.11 m/s

|V₂| =  = 66.1 m/s

 

Infine, avendo tutto il necessario, calcoliamo l’angolo adiacente alla velocità assoluta in uscita dalla girante:

 = 25.46°

 

In realtà l’angolo di uscita del fluido non corrisponde esattamente a . Questo fatto è dovuto principalmente alla viscosità del fluido. L’angolo che risulta in uscita differisce leggermente da e viene chiamato  geometrico (_g).

Per trovare questo angolo partiamo dalla definizione di slip factor:

“lo slip factor è il rapporto tra la velocità effettiva del vortice (componente tangenziale della velocità del fluido) e la velocità teorica del vortice stesso (componente di velocità tangenziale teorica)” [Wikipedia].

Può essere scritto con la seguente formula :

 

 

 

  si può trovare così:

Tale valore rappresenta la velocità ideale allo scarico con un numero infinito di pale.

Combinando le formule date dal testo con il valore dello slip factor, riusciamo a ricavarci dalla seguente relazione il valore di b₂ geometrico:

 

 

Imponendo che lo slip factor si avvicini il più possibile a zero, mediante il risolutore di Excel, otteniamo  b_2g = 129,135 °.

 

Troviamo adesso la velocità allo scarico del diffusore V₃. Per fare ciò facciamo il bilancio energetico sul diffusore stesso, tenendo conto della relazione che definisce il diametro D₃=2 D₂.

 

Applichiamo il teorema di Bernoulli:

 

 

 

 

Dove =       e       = V₃²/2 * x _diff

 

L’incognita p₂ è facilmente ricavabile dall’equazione di conservazione dell’energia sul sistema di riferimento relativo.

 

 

 

Dove l_w,gir= x _gir * = 303.16 J/Kg

 

 

Non conosciamo ancora p₁, facciamo quindi l’equazione di Bernoulli sul distributore

 

 

Ed invertendo la formula troviamo adesso sostituendo quest’ultimo termine trovato al bilancio relativo, ricaviamo 

Successivamente ricaviamo  V₃ dal bilancio sul diffusore:

 

V₃= 30,86 m/s.

 

Avendo trovato la velocità allo scarico del diffusore possiamo trovare  ,pari a 95,23 J/kg.

Abbiamo quindi tutti i dati per trovare il rendimento idraulico effettivo: