Analisi FEM

Analisi modale

Decidiamo di eseguire sull’albero un’analisi modale in Autodesk Inventor al fine di individuare i modi di vibrare e le frequenze proprie realizzando così un confronto con i risultati ottenuti nel corso di vibrazioni.

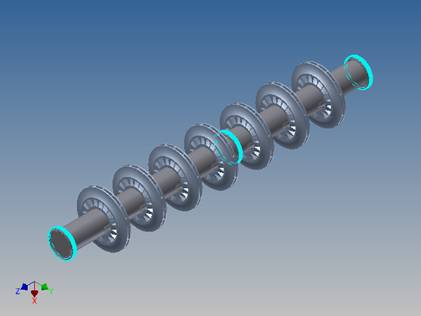
I vincoli applicati all’assieme per eseguire l’analisi (visibili in figura) sono vincoli pin che bloccano completamente il movimento degli anelli esterni dei cuscinetti; la rigidezza dei cuscinetti è stata modellizzata con dei contatti di tipo molla applicati agli anelli esterni ed interni dei cuscinetti.

Frequenza F11 748.4 Hz F12 985.71 Hz F13 994.05 Hz F14 1352.03 Hz F15 1516.23 Hz F16 1517.07 Hz F17 1687.04 Hz F18 1913.82 Hz F19 2096.41 Hz F20 2113.77 Hz

Risultati dell’analisi:

	Frequenza
F1	88.37 Hz
F2	88.41 Hz
F3	98.06 Hz
F4	138.95 Hz
F5	139.02 Hz
F6	275.22 Hz
F7	276.42 Hz
F8	344.29 Hz
F9	557.10 Hz
F10	559.29 Hz

Le frequenze proprie, come previsto, risultano diverse da quelle calcolate per il corso di vibrazioni presumibilmente a causa del fatto che è stata eseguita un’analisi del moto flessionale nello spazio invece che nel piano. Si nota che alcuni valori delle frequenze proprie coincidono con i valori calcolati col modello a parametri concentrati utilizzato nella parte di meccanica delle vibrazioni.

Calcolando la frequenza di rotazione a regime dell’albero

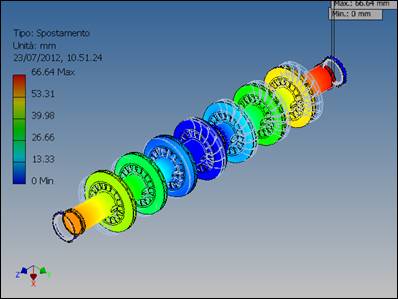
 si nota che questa frequenza è molto vicina alle frequenze proprie associate al quarto e al quinto modo di vibrare; di conseguenza la deformata del sistema a regime sarà presumibilmente simile alle deformate del quarto e del quinto modo di vibrare.

Figura 5: Deformata del 4° modo di vibrare

 

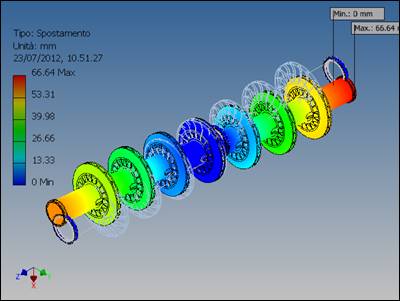
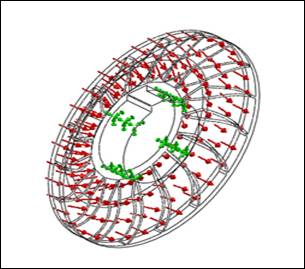
Figura 6: Deformata del 5° modo di vibrare

Analisi fluidodinamica sulla girante

Eseguiamo ora un’analisi fluidodinamica delle giranti in SolidWorks per validare in parte i parametri di progetto calcolati per il corso di macchine.
Dato che la differenza delle pressioni a monte e a valle di una singola girante è la stessa per tutte e sette le giranti decidiamo di condurre l’analisi solo sul primo stadio della pompa e, sfruttando i calcoli di progetto (vedi corso di macchine), si ottiene il seguente risultato:

 

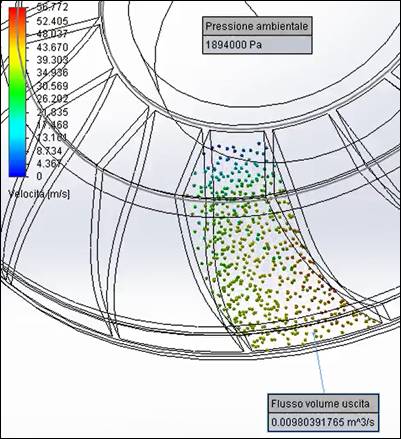
Figura 7: Simulazione fluidodinamica nel canale palare

Parametri  utilizzati per la simulazione:   Si è deciso di effettuare l’analisi all’interno di un unico canale palare per avere una maggiore concentrazione di sferette che migliorassero la comprensione del profilo di velocità.

Dalla figura è visibile l’andamento del profilo di velocità del fluido, in particolare , si può notare dove il fenomeno della cavitazione e del “distacco di vena” possono verificarsi.
Il distacco di vena è dovuto al progressivo rallentamento dell’acqua all’interno del canale palare causato dal fatto che parte dell’energia cinetica è trasformata in energia di pressione.
Viceversa la cavitazione può instaurarsi nelle zone di bassa pressione (alta velocità) qualora essa sia inferiore alla pressione di saturazione del fluido.
Il report del programma fornisce un valore di velocità massima pari a 52.7 m/s e tale valore risulta paragonabile con i moduli delle velocità relative calcolate in fase di progetto.

 

Analisi strutturale della girante

E’ possibile condurre sulla girante un ulteriore analisi di deformazione causata dalla pressione che agisce sulle pale della girante stessa. Per fare questo abbiamo applicato sulla superficie opposta alla direzione di ingresso del fluido la pressione  che corrisponde al massimo valore assunto dalla pressione del fluido all’interno del canale palare.

 

Anche in questo caso i vincoli che sono stati applicati alla geometria per eseguire l’analisi sono quelli garantiti dall’assemblaggio ed in particolare è stato vincolato lo spostamento lungo l’asse e la rotazione libera attorno all’albero (vincolo pin). Assegnando al componente il materiale  X5 CrNi 13-4, il quale presenta una resistenza alla trazione di 760-960 N/mm2  e un valore di snervamento maggiore di 550 N/mm2 , si ottiene:

Figura 8: Vincoli e carichi agenti sulla girante

 

Tabella 5: Sforzi e spostamenti agenti sulla girante

 

Come è possibile notare il valore massimo di sforzo è inferiore allo sforzo di snervamento del materiale. Dalle analisi risulta anche un valore del coefficiente di sicurezza (calcolato con la sollecitazione massima di von Mises) molto maggiore di uno quindi, sotto le ipotesi considerate, la girante non dovrebbe avere problemi di resistenza meccanica.

 

Maggiori dettagli e informazioni sono ricavabili dai disegni tecnici e dai file allegati al progetto (vedi appendice A).