Ground Interceptor Drone

Drone terrestre per applicazioni industriali

Sfruttando gli strumenti messi a disposizione dal Politecnico di Milano abbiamo eseguito alcune analisi FEM di componenti critici del GID tramite Autodesk Inventor@ Professional 2016. Queste analisi sono di prima approssimazione ma possono fornire indicazioni su dove migliorare eventuali versioni future del drone o dove prestare maggiore attenzione in fase di costruzione e utilizzo.

I risultati numerici delle simulazioni sono così riassumibili:

Albero di trasmissione: in acciaio 440C, sottoposto ad una coppia di 3Nm, ad una forza peso di 63,7N dovuta al drone e di 15,7N dovuta alla ruota ha subito uno spostamento massimo di 0,002mm e sforzo di Von Mises massimo di 25,7MPa. Il coefficiente di sicurezza risultante è di oltre 15, che è giustificato dall'aver eseguito una verifica statica.
La verifica a fatica è stata effettuata imponendo il limite a vita infinita sulle curve di Woheler.

Scocca inferiore: in ABS, sottoposta ad un carico di 78,4N sulla base e di 29,4N sui supporti laterali ha subito uno spostamento massimo di 0,145mm e sforzo di Von Mises massimo di 0,862Mpa. I coefficiente di sicurezza risultante è di oltre 15.

Ruota: in alluminio 6061, per il suo studio abbiamo utilizzato due diverse modellizzazioni: una per gli ottenere gli sforzi e una per le deformazioni. Per i primi è stato considerato fisso lo pneumatico ed è stata applicata una coppia di 3Nm all'asse oltre al peso di 78,4N, mentre per le deformazioni si è utilizzato un modello leggermente modificato con una superficie liscia di contatto con il suolo considerata fissa e stessi carichi del caso precedente.
Ne è risultata una deformazione massima di 0,23mm e uno sforzo massimo di 1,71MPa. Il coefficiente di sicurezza risultante è di oltre 15, ma valgono le stesse considerazioni sulla vita a fatica fatte per l'albero.
Non è stato possibile simulare urti sulle ruote, ma si è scelto lo pneumatico anche considerando questo tipo di sollecitazione.

Per visionare le immagini in dimensione originale e per analizzare nel dettaglio la mesh utilizzata è possibile cliccare qui.

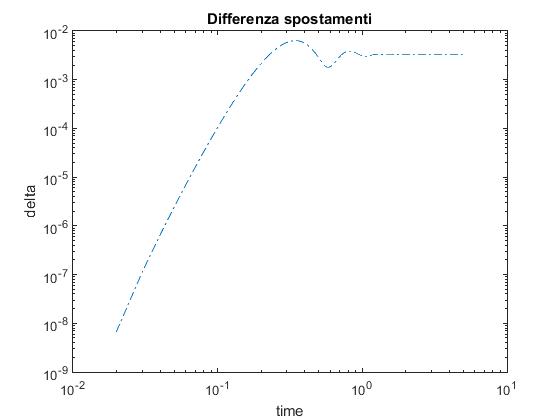
Spostamenti nell'albero di trasmissione	Sforzi di Von mises nell'albero di trasmissione
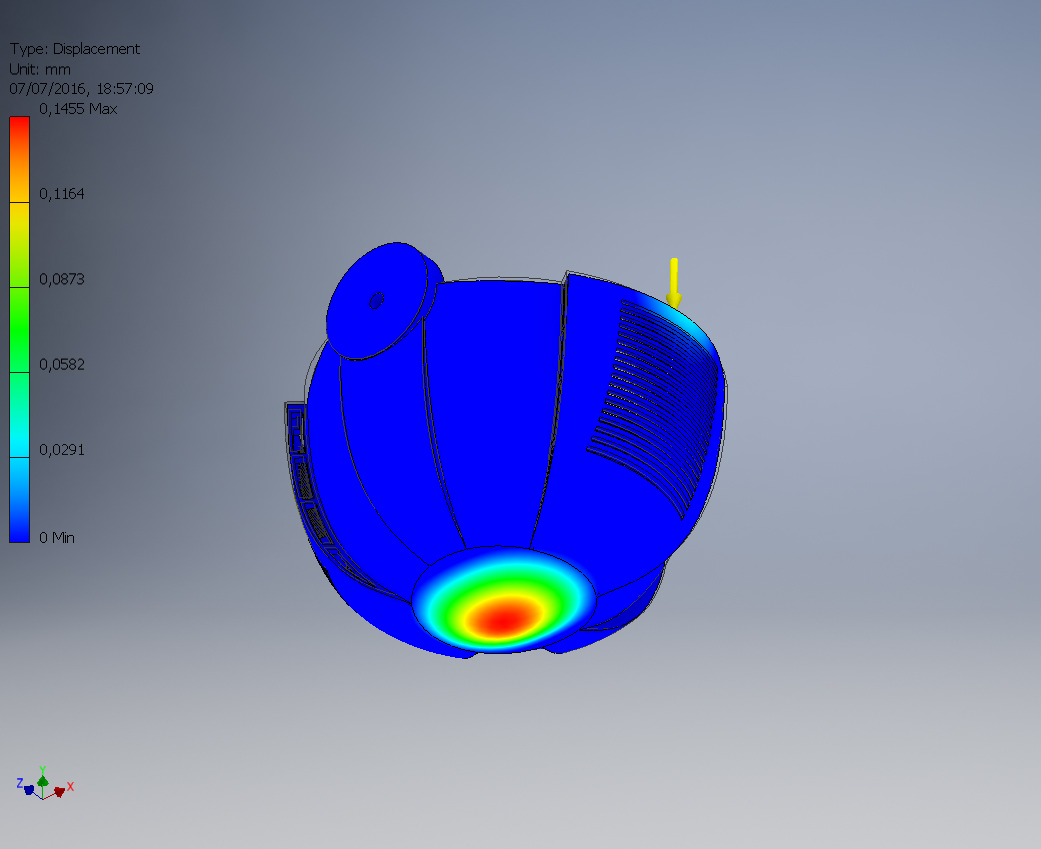Spostamenti nella scocca	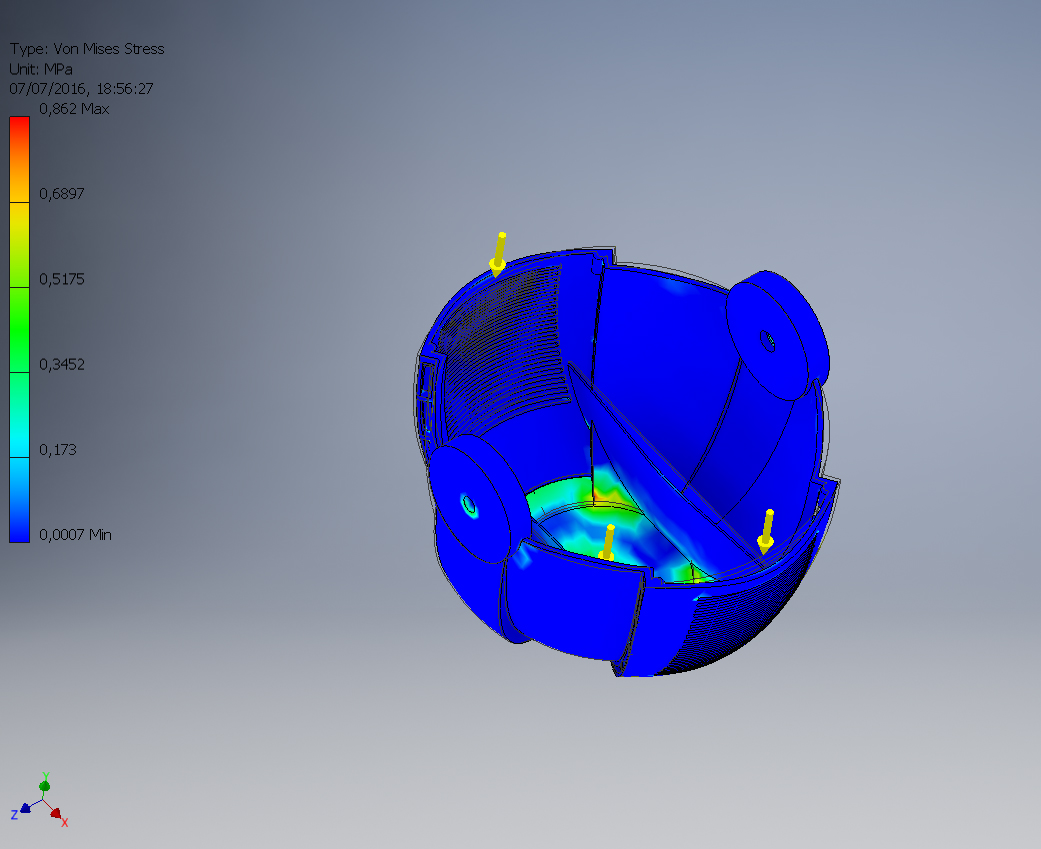Sforzi di Von Mises nella scocca
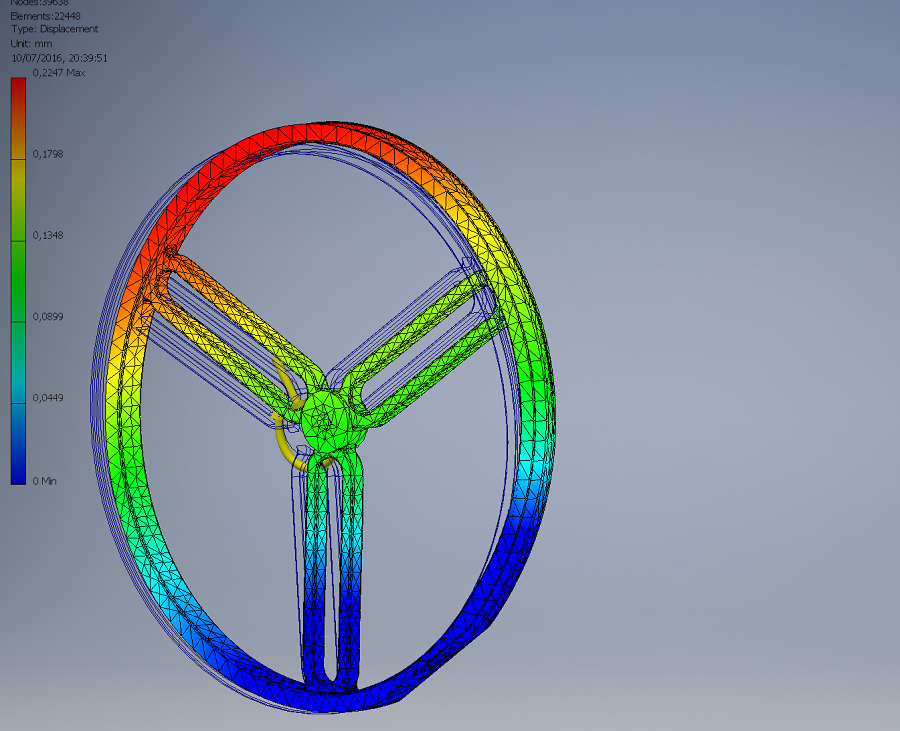Spostamenti nella ruota	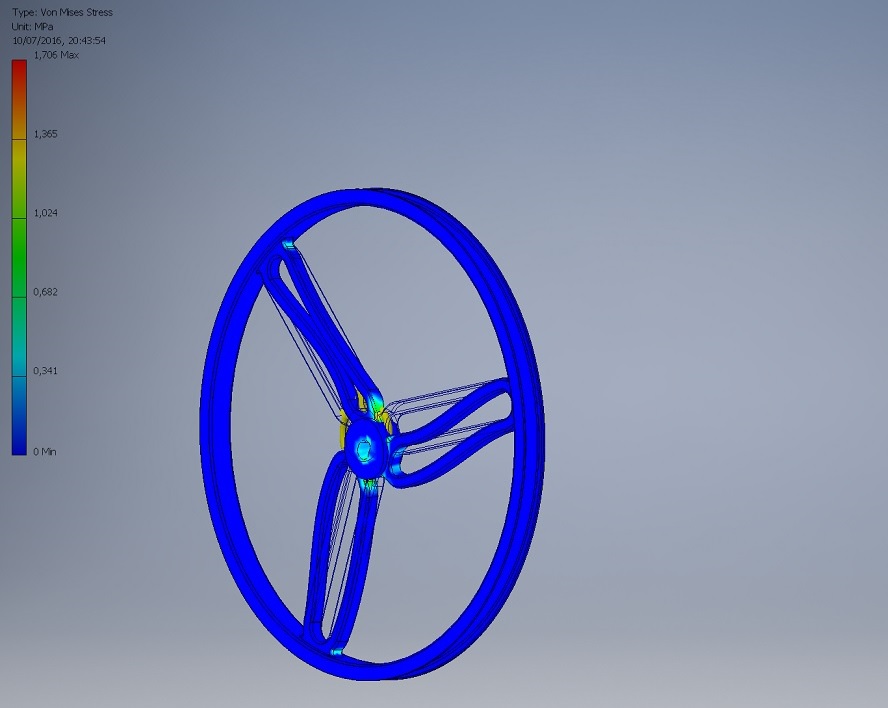Sforzi di Von Mises nella ruota

Per quanto riguarda il controllo dell’entità delle oscillazioni abbiamo simultao un sistema in retroazione PID (Proporzionale-Integrale-Derivativo) tramite il sorftware Matlab@ R2015a Accademic.
Il funzionamento del sistema è il seguente: l’input fornito dal giroscopio, che fornisce il valore attuale della posizione angolare, permette di reagire a un eventuale errore positivo o negativo facendo variare la coppia fornita dal motore, tendendo verso la posizione di equilibrio.
Il PID regola l'uscita in base al valore del segnale di errore (azione proporzionale), i valori passati del segnale di errore (azione integrale) e a quanto velocemente il segnale di errore varia (azione derivativa).
Le tre azioni di un PID vengono calcolate separatamente e semplicemente sommate algebricamente.

Il controllo sul motore può essere paragonato a un pendolo, con massa pari e metà di quella totale del drone, sottoposto a un’accelerazione iniziale pari a 1 m/s^2. Abbiamo quindi valutato rigidezza e smorzamento equivalenti che il controllo deve fornire per fermare l’oscillazione in 1s e limitarla a un massimo di 4» (data l’oscillazione ridotta, possiamo usare equazioni linearizzate).
I valori trovati sono: k=50 N/m ed r=3 m/s.

Progetto svolto dal Team 576 del Laboratorio Sperimentale CAD 2016 con la supervisione del prof. Gaetano Cascini e dell'ing. Edoardo Filippo Colombo