Dopo aver acquisito i dati relativi al valore assunto dalla pressione dell'aria all'interno del cilindro, passiamo ad elaborare un modello

per calcolare le perdite di carico. Innanzitutto sottolineiamo che questo modello è adatto per il calcolo delle perdite di carico a basse velocità.

Questo perchè, per basse velocità, si instaura una condizione di regime e quindi la differenza di pressione tra i cilindri e il regolatore di

precisione è interamente dovuta alle perdite di carico del circuito. Viceversa, per alte velocità, il modello da noi elaborato si discosta dalla

realtà perchè la caduta di pressione non è determinata dalle perdite di carico, ma dal fatto che il sistema non è sufficiente a far fluire la

portata e quindi si crea una sorta di "ingorgo" dovuta al fatto che il diametro dei tubi è troppo piccolo. Per questo, l'aria incontra difficoltà

nel fluire all'interno del circuito.

Nel blocco verde riportiamo i dati del problema che ci consentiranno di determinare la caduta di pressione. Per tubo 1 intendiamo i due

tubi che collegano i cilindri con il raccordo a T, mentre il tratto di tubo in comune collega il raccordo a T al regolatore di precisione.

Passiamo ora al calcolo delle perdite di carico. Le perdite di carico distribuite si hanno nei tubi rilsan, ovvero nel tubo 1 e nel tubo in comune,

mentre le perdite di carico localizzate si concentrano in prossimità del raccordo a T e degli intercettatori di blocco.

I tubi rilsan si possono considerare lisci. Nel blocco giallo calcoliamo le perdite di carico nel tubo 1 e nel tratto di tubo in comune.

Per calcolare la velocità nel circuito 1 (v_C) applichiamo la continuità, ovvero sfruttiamo il fatto che le portata resta costante.

 

                                              

                                                          

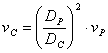
Nota la velocità nel tubo è possibile calcolare la portata, il numero di Reynolds e il numero di Mach. Le formule che utilizziamo sono le seguenti e

valgono solo in caso di Ma < 0,3:

Noto il numero di Reyolds, è possibile calcolare il regime di moto dell'aria all'interno dei tubi confrontando il valore ottenuto con quello critico

pari a 2000. Per Re > 2000 il moto è turbolento, per Re < 2000 il moto è laminare. Noto il numero di Mach impostiamo il modello di calcolo delle

perdite di carico. Se Ma < 0,3 allora è possibile elaborare un modello di flusso incomprimibile, se Ma > 0,3 si deve adottare un modello a flusso

comprimibile. v_S è la velocità del suono nel mezzo (aria) e vale 340 m/s. In entrambi i tratti di tubo è corretta l'ipotesi di flusso incomprimibile e

il regime di moto è turbolento. In queste condizioni è possibile determinare il fattore di resistenza per moto turbolento con la formula:

Qualora il flusso fosse in moto laminare si avrebbe un diverso fattore di resistenza determinabile tramite la formula:

Noto il fattore di resistenza calcoliamo la perdita di carico che interessa il tratto di tubo analizzato con la formula:

sono proporzionali alla portata al quadrato. Per determinarle abbiamo quindi utilizzato la seguente formula:

Il coefficiente di proporzionalità C è stato dedotto dalla letteratura. La perdita di carico localizzata totale data dalla somma delle perdite che

si hanno nell'intercettatore di blocco e nel raccordo a T.

La perdita di carico totale data dalla somma di quella distribuita e localizzata è stata calcolata nel blocco viola.

Ora che abbiamo calcolato le perdite di carico valutiamo la correttezza del modello adottato. Per far ciò dobbiamo confrontare il modello teorico

che abbiamo realizzato con i dati sperimentali rilevati. Consideriamo il circuito completo nel quale abbiamo le perdite di carico distribuite e

localizzate, la caduta di pressione dell'intero circuito è proporzionale alla portata al quadrato e la relazione che consente di calcolarne il valore è:

C è un coefficiente di proporzionalità globale, ovvero esteso a tutto il circuito. Quello che faremo è calcolare la caduta di pressione sia teorica che

sperimentale al variare della velocità del pistone e, poiché la portata è nota, risalire ai valori sia del coefficiente teorico che sperimentale.

La caduta di pressione teorica si calcola a partire dal foglio di calcolo sopra riportato variando le velocità del pistone, la caduta di pressione

sperimentale si calcola a partire dai dati acquisiti in precedenza valutando la differenza tra il massimo valore di pressione raggiunto nel cilindro e

la pressione letta dal regolatore di precisione.   

Come precedentemente detto il legame tra le due grandezze è parabolico, aggiungendo la retta di tendenza osserviamo il valore dei coefficienti

 teorico e sperimentale. Otteniamo:

Osservando il grafico possiamo concludere che il modello teorico che abbiamo creato per quantificare le perdite di carico che si hanno lungo il

 circuito è sufficientemente corretto, in particolare, sottolineiamo che il modello risulta ottimo per basse velocità. Questo risultato non è casuale e

 inaspettato, ma è in accordo con quanto detto all'inizio della pagina, dove avevamo anticipato che solo per basse velocità la caduta di pressione era

 imputabile alle perdite di carico.

 

torna su