ANALISI FEM
Lo scopo dell’analisi consiste nell’alleggerire la struttura, cercando una sezione che fornisca le stesse prestazioni di quella attuale. In questo modo si otterrà una struttura più leggera, più facile da lavorare e da spostare e anche più economica
L’idea è quella di costruire una mensola in cui l’elemento strutturale principale è un tubolare che a parità di volume e quindi di peso, è quello che resiste maggiormente alle sollecitazioni di torsione. Tale scelta è vantaggiosa e permette di raggiungere più obbiettivi:
| si riducono i pesi della struttura che risulta più manovrabile |
| si diminuiscono le sollecitazioni a cui è sottoposta la vite a ricircolo di sfere |
| la sezione tubolare è un componente commerciale quindi risulta economicamente vantaggiosa |
| si diminuisce il numero delle lavorazioni di carpenteria necessarie |
La mensola viene completata con l’aggiunta di elementi di giunzione sempre tagliati al laser (Figura.1)
Il metodo con cui affrontare il problema è quello di analizzare il manipolatore nella configurazione peggiorativa, quella cioè che sottopone la mensola alla massima torsione.
E’ importante evidenziare che in elementi di macchine di questo tipo, il vincolo di progettazione non è la resistenza meccanica, ma la rigidità strutturale. In questo caso essa dovrà essere tale da garantire un’abbassamento massimo della massa traslante (Ymt). Tale vincolo sarà quello su cui verrà basato il dimensionamento del componente.
L’abbassamento massimo del pezzo in presa al manipolatore è una grandezza che non ci è stata fornita, ma la specifica che l’azienda ci ha chiesto di rispettare è quella di ottenere un carrello verticale caratterizzato da prestazioni simili a quelle attuali. Mediante l’analisi FEM del carrello attuale possiamo ricavare la sua massima deformata e il conseguente abbassamento della massa traslante che sarà dato da due contributi:
· un abbassamento dovuto alla flessione
· una rotazione dovuta alla torsione
Il software utilizzato per l’analisi FEM è ABAQUS 6.4-1. Tale scelta è stata dettata soprattutto da motivi didattici, infatti esso è un programma che è stato trattato durante il percorso di studio svolto in corsi di Costruzione di Macchine e per questo motivo era disponibile nei vari laboratori della sede Piacentina del Politecnico di Milano.
Nello specifico, la sezione utilizzata per l’analisi è quella denominata ABAQUS.CAE e consente di
| Creare la geometria |
| Assegnare i vincoli |
| Lanciare l’analisi |
Una utile caratteristica del programma consiste nel fatto che è possibile importare la geometria del modello attraverso un file generato con i più importanti e comuni programmi di modellazione come SOLID EDGE.
Il modulo CAE contiene varie funzioni che sono disposte nella corretta sequenza con cui si deve affrontare un’analisi di questo tipo, di seguito si riporta una sintetica descrizione delle principali:
o Part
Consente di creare la geometria del modello da analizzare: in pratica contiene gli essenziali comandi di un comune modellatore solido
o Property
In questa sezione si assegnano le caratteristiche ai vari materiali in gioco e li si associano alle varie parti dell’elemento/assieme oggetto dell’analisi
o Assembly
In questo ambiente si assembla il modello quando questo è costituito da più parti modellate singolarmente
o Step
Consente di definire il tipo di analisi che si vuole effettuare (statica lineare, statica non lineare, dinamica, ….) e inoltre si può suddividere l’analisi in varie fasi
o Interaction
Si assegnano i vincoli che le varie parti di un assieme si scambiano
o Load
Si assegnano i vincoli e i carichi a cui la struttura complessiva è soggetta
o Mesh
E’ la sezione più importante, serve per definire il tipo di elemento che si vuole utilizzare e la disposizione di essi nella struttura. Il risolutore contiene degli algoritmi che consentono di ottenere una mesh automaticamente, ma nelle applicazioni più complesse questo metodo, anche se semplifica notevolmente il lavoro, non rappresenta una buona soluzione in quanto infittisce la mesh in punti dell’elemento in cui non serve un’attenta analisi. Nel caso di strutture semplici questo non causa problemi, ma se l’elemento è complesso lo sforzo computazionale può risultare inutilmente laborioso. Per questo motivo ci sono dei controlli denominati SEED che consentono di definire il numero e la disposizione dei nodi in ogni parte dell’elemento. In questo caso entra in gioco l’abilità del progettista che deve individuare i punti in cui è necessario avere molti elementini che sono quelli in cui ci sono i maggiori gradienti di sforzi/deformazioni e conseguentemente quelli in cui è possibile risparmiare mesh.
o Job
In questo ambiente si definisce il file di imput al risolutore e si lancia l’analisi
o Visualization
Serve per visualizzare i risultati dell’analisi a schermo
Le fasi seguite sono le stesse descritte precedentemente, ma si darà risalto a quelle salienti; alcune di esse infatti non sono neanche state utilizzate in quanto non necessarie.
Il primo passo è stato quello di importare il file contenente la geometria della struttura. Solid Edge permette di generare file di formato “.igs” che sono leggibili da Abaqus.
Successivamente sono state definite le caratteristiche del materiale Fe 360:
- E=260000 N/mm2
- ν=0.3
Questa fase è molto importante in quanto definisce le forze a cui è soggetta la struttura e come essa è vincolata. Bisogna tenere conto dei pesi delle varie parti che ci sono stati forniti dall’azienda:
I carichi da applicare sono ovviamante quelli risultanti quando la massa traslante è posizionata nel punto più distante dal carrello. Il momento torcente sarà costituito da due contributi:
· Peso della massa traslante moltiplicato per la lunghezza del profilo
· Peso del profilo moltiplicato per la metà della lunghezza del profilo
Considerando che:
· Massa traslante = 100 kg
· Massa del profilo = 56.24 kg
· Massa del carrello orizzontale = 58.9 kg
· Lunghezza del profilo = 2850 mm
Si ricava:
Mt =9.81[(100 ·2850)+(56.24 · 2850/2)]=3582000 N·mm
La forza verticale sarà data dalla somma delle forze peso della massa traslante, del profilo e del carrello orizzontale:
Fv=9.81 · (100+56.2+58.9)=2100 N
Viene inoltre imposto il vincolo di incastro alla superficie del carrello che è a contatto con le guide.
Nel nostro caso la geometria in gioco e abbastanza semplice, quindi è possibile applicare la meshatura automatica. Come elementi per l’analisi si scelgono quelli tetraedrali (figura 1 ) in quanto sono quelli che meglio si adattano ad una geometria generica, e che generalmente non danno luogo a problemi di distorsioni.

Figura 1
A questo punto è possibile lanciare l’analisi e visualizzare i risultati.
In figura 2 è rappresentato il comportamento della struttura. Per quanto riguarda i risultati si deve considerare che l’abbassamento della massa traslante (Ymt) sarà il risultato di due contributi:
| la rotazione della sezione dovuta alla torsione provocata dal momento torcente Mt | |
| l’abbassamento della sezione dovuta alla flessione provocata dalla forza Fv |

Figura 2
E’ quindi necessario visualizzare due grandezze:
| lo spostamento verticale della sezione lungo la direzione 3 (U3) | |
| la rotazione della sezione attorno alla direzione 1 (UR1) |
In figura 3 e 4 sono visualizzati i valori di queste grandezze per tutta la struttura con la modalità a colori tipica dell’analisi FEM.
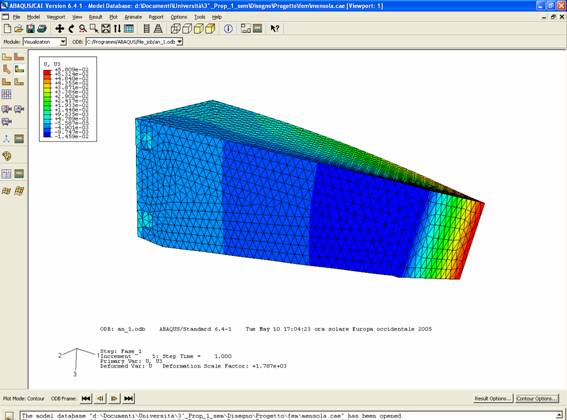
Figura 3
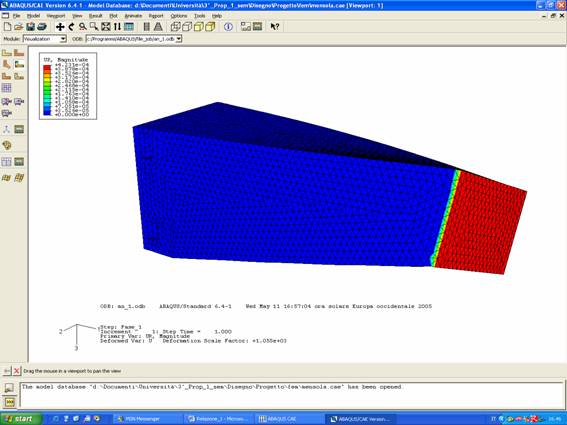
Figura 4
Considerando il nodo centrale della sezione si ottiene
| U3 = 0.0218802 mm | |
| UR1 = 0.000421067 rad |
Da questi due valori è semplice ricavare lo spostamento verticale della massa traslante
Ymt=(Ymt-mom_torc+Ymt-F_vert)=(0.0218802)+(2850 ·0.000421067)=1.2 mm
E’ importante notare che il contributo flessionale che è quello dato dalla forza verticale, è molto più piccolo di quello torsionale
![]()