![]()
Progettazione
Questa sezione è suddivisa nei seguenti sottocapitoli:
| dimensionamento della trasmissione a cinghia; | |
| analisi delle forze agenti; | |
| verifica dell'inflessione; | |
| componenti supplementari di collegamento. |
Tutti i calcoli effettuati nella progettazione sono riportati nel seguente foglio di calcolo: Miscelatore.xls.
![]()
Dimensionamento della trasmissione a cinghia
Si sceglie una cinghia di tipo trapezoidale per ragioni di comodità, di costo e perché il rapporto di trasmissione è compreso tra 1 e 6, quindi è relativamente basso.
Per una corretta scelta della cinghia si usa come riferimento il catalogo KOMPATTEX della Pirelli.
Le condizioni di funzionamento prevedono una maggiorazione della potenza da trasmettere in base al tipo di funzionamento.
Nel nostro caso l’azionamento è dato da un motore elettrico a c.a. e si prevede un funzionamento dell’agitatore per 20 ore giornaliere. Secondo questi dati, il coefficiente di correzione è c = 1.3, quindi la potenza corretta è
![]()
Una volta noto il rapporto di trasmissione, si sceglie il diametro della puleggia condotta D e si trova quello della puleggia motrice d considerando; di conseguenza cambieranno anche il rapporto di trasmissione e il numero di giri dell’albero. Dati i valori di potenza molto vicini, risulta opportuno scegliere un medesimo modello di cinghia per entrambi i tipi di fluido:
|
|
Liquido
A |
Liquido
B |
|
c
= |
1,3 |
1,3 |
|
Pc
[kW] = |
20,434 |
28,850 |
|
Tipo
di cinghia |
5V |
|
|
D
[mm] = |
355 |
|
|
d
[mm] = |
280 |
|
|
t' = |
1,27 |
|
|
n'
albero [rpm] = |
225,96 |
|
Sempre considerando le indicazioni del catalogo, si procede alla determinazione dei parametri caratteristici della trasmissione a cinghia:
|
Interasse provvisorio [mm]: |
![]()
|
Lunghezza esterna provvisoria [mm]: |
![]()
|
Lunghezza esterna nominale [mm]: |
![]()
|
Interasse effettivo [mm]: |
![]()
|
Lunghezza esterna reale [mm]: |
![]()
|
Angolo di avvolgimento della puleggia motrice: |
![]()
|
Angolo di avvolgimento della puleggia condotta: |
![]()
Ora si può passare
al calcolo dei dati dinamici, per verificare il momento resistente e il numero
di cinghie; T e t rappresentano i tiri rispettivamente della parte superiore e di
quella inferiore della cinghia, il coefficiente di attrito fra cinghia e
puleggia è pari a m =
0.5
.
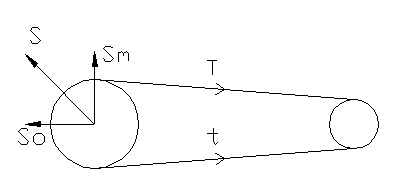
Il momento
resistente è dato dal rapporto dalla potenza assorbita dal fluido e dalla
velocità angolare dell’albero Mr = W/wm
; considerando però l’equilibrio delle forze nel sistema costituito dalle due
pulegge, si ottiene la seguente equazione:
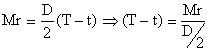
Il tiro esercitato dalla cinghia sull’albero è dato dalla composizione del tiro So (agente sulla retta congiungente i centri delle due pulegge) e Sm (agente perpendicolarmente a So). Il numero delle cinghie deriva dal fatto che esse possono trasmettere una potenza massima trasmissibile Pmax, data dal prodotto dalla coppia massima trasmissibile Mr,max per la velocità angolare dell’albero. Il numero di cinghie è dato dal rapporto della potenza trasmessa da una cinghia e la potenza trasmessa dalla cinghia nelle reali condizioni di esercizio.
![]()
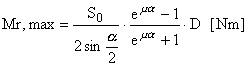
|
|
Liquido
A |
Liquido
B |
|
Mr
[Nm] = |
523,958 |
739,734 |
|
T-t
[N] = |
2951,877 |
4167,514 |
|
So
[N] = |
4427,815 |
6251,271 |
|
Mr,max
[Nm] = |
787,212 |
1111,400 |
|
Pc
[kW] = |
18,627 |
26,298 |
|
n°
cinghie = |
2 |
2 |
Per le cinghie tipo 5V il catalogo Kompattex impone i seguenti valori:
| A = 15 mm | |
| S = 13 mm | |
| a = 40° |
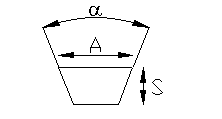
Ora si può calcolare la componente del tiro perpendicolare all’interasse delle pulegge e quindi il tiro esercitato sull’albero:
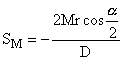
![]()
|
|
Liquido
A |
Liquido
B |
|
Mr
[Nm] = |
4427,815 |
6251,271 |
|
T-t
[N] = |
167,914 |
237,064 |
|
So
[N] = |
4430,998 |
6255,765 |
Il momento
resistente allo spunto deve essere il doppio del momento torcente nominale, in
quanto solitamente all’accensione la coppia erogata dal motore deve essere
più elevata per vincere le resistenze iniziali dell’utilizzatore (nel nostro
caso il fluido da miscelare).
La dimensione delle pulegge sarà nota una volta calcolato il diametro dell’albero sul quale andrà calettata la puleggia.
Analisi delle forze agenti
Per procedere all’analisi delle forze statiche (azioni interne e reazioni vincolare), dovute alla sola azione delle pale, bisogna schematizzare l’albero con uno schema a travi, distinguendo i carichi nei piani x-z e y-z.
Piano x-z
Le pale esercitano un carico composto da una componente P in direzione assiale e una componente 0.2P in direzione radiale rispetto all’asse dell’albero; questi carichi sono applicati a una distanza di 2/3 la lunghezza della pala partendo dalle estremità e non variano nel tempo anche se l’albero ruota.
Dalla precedente raffigurazione si nota che i due cuscinetti di supporto sono schematizzati da un carrello e una cerniera; infatti, a partire dalla puleggia della cinghia, il primo cuscinetto fornisce un vincolo radiale (impedisce all’albero di spostarsi radialmente) e il secondo un vincolo assiale (impedisce all’albero di spostarsi assialmente). Essendo i due carichi P in direzione opposta l’uno rispetto all’altro, non si ha alcuna azione assiale e nemmeno radiale sulla parte dell’albero superiore al giunto.
Essendo il carico radiale molto inferiore di quello assiale, lo si trascura e si calcola P partendo dalla coppia esercitata, in quanto si conosce la potenza W assorbita dal fluido.
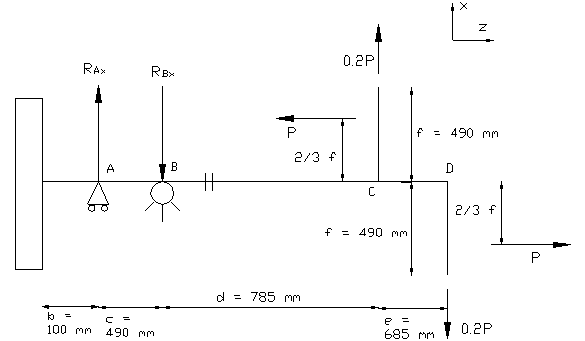
Carichi applicati:
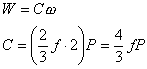
![]()
![]()
![]()
Momenti flettenti e torcenti:
![]()
![]()
![]()
![]()
![]()
|
|
Liquido
A |
Liquido
B |
|
Potenza
ass, [kW] = |
15,719 |
22,192 |
|
P
[N] = |
1016,792 |
1435,526 |
|
RAx
[N] = |
1071,436 |
1512,673 |
|
RBx
[N] = |
1071,436 |
1512,673 |
|
MfB
[Nmm] = |
525003,582 |
741209,740 |
|
MfC
[Nmm] = |
192851,542 |
272271,363 |
|
MfD
[Nmm] = |
332152,040 |
468938,376 |
|
MtA
[Nmm] = |
664304,080 |
937876,752 |
|
MtB
[Nmm] = |
332152,040 |
468938,376 |
Piano x-y
In questo piano le
pale esercitano la sola azione assiale P,
quindi non ci sarà momento torcente. Come per il piano x-z, si rappresentano i
diagrammi di momento flettente e di taglio, mentre non c’è né momento
torcente né azione assiale in quanto le pale esercitano una sola reazione di
componente radiale.
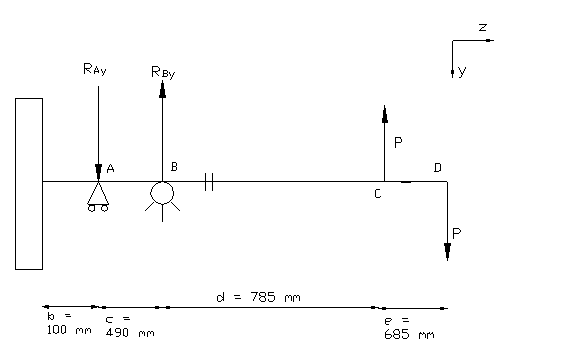
Equilibrio delle
azioni interne:
![]()
![]()
![]()
![]()
|
|
Liquido
A |
Liquido
B |
|
Potenza
ass, [kW] = |
15,719 |
22,192 |
|
P
[N] = |
1016,792 |
1435,526 |
|
RAy
[N] = |
-1421,43366 |
-2006,806254 |
|
RBy
[N] = |
-1421,43366 |
-2006,806254 |
|
MfB
[Nmm] = |
696502,492 |
983335,0645 |
|
MfC
[Nmm] = |
696502,492 |
983335,0645 |
Composizione dei due piani
Nel corso del dimensionamento dell’albero e di tutti i suoi componenti, i precedenti valori di azioni interne e reazioni vincolari andranno a seconda dei casi considerati singolarmente piano per piano oppure nelle loro composizioni; infatti i due piani x-z e y-z sono tra loro perpendicolari e per ogni zona di sezione dell’albero è possibile determinare un corrispondente valore di composizione secondo il teorema di Pitagora dei momenti flettenti o delle azioni di taglio.
Al fine del
dimensionamento dell’albero è utile conoscere le composizioni del momento
flettente massimo e delle azioni dovute ai cuscinetti, mentre il momento
torcente resta quello relativo al piano x-z:
![]()
![]()
![]()
|
|
Liquido
A |
Liquido
B |
|
RA
[N] = |
1780,014 |
2513,056 |
|
RB
[N] = |
1780,014 |
2513,056 |
|
Mf
[Nmm] = |
872206,674 |
1231397,469 |
|
MT
[Nmm] = |
664304,080 |
937876,752 |
![]()
Verifica dell'inflessione
Quando tutto il sistema è in esercizio, l’albero sarà soggetto ad una deformazione, la quale all’estremità delle palette non dovrà superare i 5 mm e nella zona compresa fra i due cuscinetti la distanza c/3000, cioè 0.163 mm. Invece la rotazione alle estremità dei cuscinetti dovrà essere minore di 1/1000 rad.
La verifica contemporanea dei tre precedenti vincoli permette di trovare il diametro minimo resistente sia dell’albero pieno esterno al fluido sia di quello cavo immerso nel fluido.
Per il calcolo della deformata si procede con il metodo dei lavori virtuali, il quale prevede di uguagliare lavoro interno e lavoro esterno a seconda delle diverse zone dell’albero per determinare i vari spostamenti o le varie rotazioni.
Bisogna però considerare due casi, uno per ciascun piano di riferimento; infatti a seconda del piano che si considera, non solo variano momento torcente e flettente, ma nel piano y-z non si ha l’influenza del tiro dovuto alla cinghia.
Un’altra distinzione è dovuta a seconda della parte di albero a cui ci si riferisce: quella immersa nel fluido è un tubo cavo in X5CrNi1810 (E=199000 Mpa, Rs=250 Mpa), mentre quella esterna è una barra circolare in Fe510 (E=210000 Mpa, Rs=360 Mpa).
Piano x-y
Per il metodo dei lavori virtuali, considerando un
carico unitario applicato in prossimità dell’ultima paletta e pensando di
spezzare l’albero nel punto in cui si trova la paletta interna, la freccia
massima è data dalla somma delle inflessioni h
nei tratti b+c+d
ed e, oltre che dalla rotazione
f
dovuta al momento flettente moltiplicata per la distanza b+c+d (la distanza
b+c+d verrà chiamata in modo
generico d):
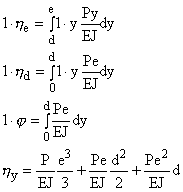
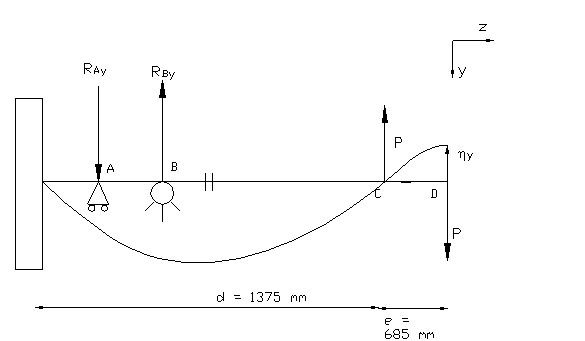
Piano x-z
In questo piano cambiano i momenti flettenti in quanto rispetto al piano precedente agiscono in più i carichi 0.2P e il tiro S.
Sempre grazie al metodo dei lavori virtuali, si ottengono le seguenti relazioni:
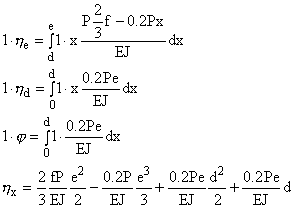
Bisogna considerare però anche la freccia e la rotazione dovuti al tiro
della cinghia:
![]()
La freccia massima fra i due cuscinetti è data dalla seguente relazione:
![]()
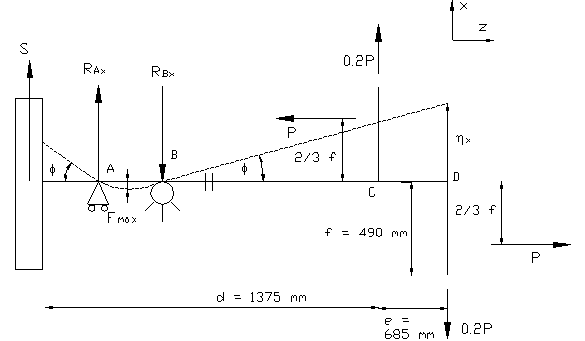
Composizione dei due piani
Il calcolo della freccia va poi considerato componendo i valori dei due piani secondo il teorema di Pitagora e verificando che il risultato non superi il limite imposto.
L’albero immerso nel fluido deve verificare la seguente condizione:
![]()
L’albero non
immerso nel fluido deve verificare le seguenti condizioni:
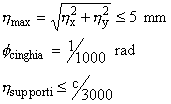
Si ottengono quindi
i seguenti valori di inflessione per l’albero immerso nel fluido (albero cavo)
e per l’albero esterno (albero pieno):
|
DIMENSIONAMENTO
DELL'ALBERO CAVO X5CrNi1810 |
E
= 199000 Mpa |
|||||||
|
h tot
<
5 mm |
||||||||
|
UNI
7091, 7288 |
Liquido
A |
Liquido
B |
||||||
|
Dest
(mm) |
Spessore |
h x |
h y |
h tot |
h x |
h y |
h tot |
|
|
114,300 |
3,200 |
1,050 |
7,951 |
8,020 |
1,483 |
11,225 |
11,323 |
|
|
139,700 |
3,600 |
0,510 |
3,858 |
3,892 |
0,719 |
5,447 |
5,494 |
|
|
168,300 |
4,000 |
0,262 |
1,980 |
1,997 |
0,369 |
2,795 |
2,819 |
|
|
193,700 |
4,000 |
0,171 |
1,293 |
1,304 |
0,241 |
1,825 |
1,841 |
|
|
DIMENSIONAMENTO
DELL'ALBERO PIENO Fe510 |
E
= 210000 Mpa |
||||||
|
h tot
<
5 mm f CINGHIA<
1/1000 rad h SUPPORTI<
c/3000 = 0.163 mm |
|||||||
|
D |
Liquido
A |
||||||
|
h x |
h y |
f CINGHIA |
h CINGHIA |
h SUPPORTI |
h tot |
||
|
65,000 |
1,022 |
7,735 |
0,0002 |
0,405 |
0,110 |
8,208 |
|
|
70,000 |
0,760 |
5,751 |
0,0001 |
0,301 |
0,082 |
6,102 |
|
|
75,000 |
0,576 |
4,364 |
0,0001 |
0,229 |
0,062 |
4,630 |
|
|
80,000 |
0,445 |
3,371 |
0,0001 |
0,177 |
0,048 |
3,577 |
|
|
D |
Liquido
B |
||||||
|
h x |
h y |
f CINGHIA |
h CINGHIA |
h SUPPORTI |
h tot |
||
|
75,000 |
0,814 |
6,161 |
0,0002 |
0,323 |
0,088 |
6,537 |
|
|
80,000 |
0,629 |
4,759 |
0,0001 |
0,249 |
0,068 |
5,050 |
|
|
85,000 |
0,493 |
3,734 |
0,0001 |
0,196 |
0,053 |
3,963 |
|
|
90,000 |
0,392 |
2,971 |
0,0001 |
0,156 |
0,042 |
3,153 |
|
Quindi i diametri
unificati corrispondenti alle inflessioni limite sono i seguenti:
|
Liquido
A |
Liquido
B |
||
|
ALBERO PIENO |
ALBERO CAVO |
ALBERO PIENO |
ALBERO CAVO |
|
D = 75 mm |
D =
139.7 mm |
D = 85 mm |
D =
168.3 mm |
Questi valori sono solamente i valori minimi resistenti; l’albero pieno avrà il diametro minimo resistente in corrispondenza della puleggia, quindi andrà aumentando a causa dei vari spallamenti dovuti al posizionamento di componenti supplementari.
E’ possibile ora
esplicitare le dimensioni delle pulegge; sempre dal catalogo KOMPATTEX, una
volta noti i valori di diametro esterno delle pulegge, il numero di cave, il
tipo di cinghie e il diametro dell’albero sul quale la puleggia verrà
calettata, si ricavano le altre quote dimensionali:
|
LIQUIDO A - B |
|
|
Puleggia condotta |
Puleggia motrice |
|
D est = 355 mm |
D est = 280 mm |
|
N° cave = 2 |
N° cave = 2 |
|
D mozzo = 100 mm |
D mozzo = 80 mm |
|
D int, mozzo = 75 - 85 mm |
D int, mozzo = 50 - 60 mm |
|
L mozzo = 60 mm |
L mozzo = 60 mm |
![]()
Componenti supplementari di collegamento
Dimensionamento del giunto
Il giunto, cioè
l’organo di collegamento fra l’albero cavo interno al recipiente e
l’albero pieno esterno, è costituito da due flange ed è soggetto a momento
flettente e torcente, mentre i bullono sono soggetti a sforzi tangenziali.
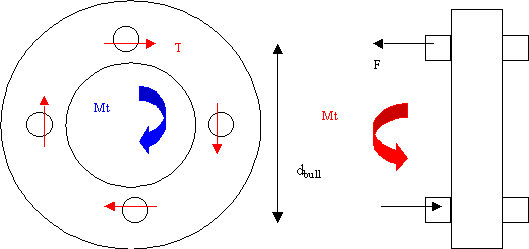
Impostando
l’equilibrio rispetto alle forze agenti sul giunto, si ottengono le seguenti
relazioni, che permettono di trovare lo sforzo assiale e tangenziale agenti sui
bulloni:
![]()
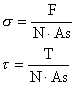
dove As è l’area resistente dei bulloni, Mf e Mt sono i momenti flettente e torcente massimi, N è il numero di bulloni.
Per esigenze dimensionali si sceglie una flangia con diametro esterno pari a 160 mm per il miscelatore funzionante con il liquido A, 190 mm per il miscelatore funzionante con il liquido B, mentre si opta per bulloni aventi classe di resistenza 4.8, cioè aventi Rs = 320 MPa, quindi
![]()
Una volta calcolati i valori di F, T, s e t dalle precedenti relazioni, si applica la teoria di Von Mises e si osserva se lo sforzo equivalente è minore di quello ammissibile.
Si fa riferimento ai valori della norma UNI 2304 riguardante le dimensioni e gli accoppiamenti fra le flange.
|
LIQUIDO
A |
|||||||||||
|
DIMENSIONI |
FORI |
F |
T |
s |
t |
s VON MISES |
s VON MISES < s
AMM |
||||
|
Øest |
Øbull |
b |
Øf |
bulloni |
N
bulloni |
||||||
|
160 |
130 |
8 |
14 |
12 |
4 |
6709,282 |
2555,016 |
14,83 |
5,65 |
17,77 |
VERO |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LIQUIDO
B |
|||||||||||
|
DIMENSIONI |
FORI |
F |
T |
s |
t |
s VON MISES |
s VON MISES < s
AMM |
||||
|
Øest |
Øbull |
b |
Øf |
bulloni |
N
bulloni |
||||||
|
190 |
150 |
8 |
18 |
16 |
4 |
8209,316 |
3126,256 |
10,21 |
3,89 |
12,23 |
VERO |
Verifica della saldatura della flangia
La verifica della saldatura andrà considerata nelle sezioni finali dell’albero pieno e dell’albero cavo che si trovano in contatto con la flangia di accoppiamento fra i due alberi. Le due flangie sono tenute insieme da quattro bulloni.
L’unione fra
l’albero cavo e la flangia è costituita da una saldatura a cordoni
d’angolo, il cui spessore deve essere verificato dalla seguente formula:
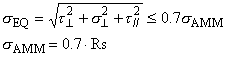
Nel nostro caso non
c’è alcun t^,
le altre due componenti sono dati dalle seguenti relazioni:
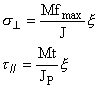
dove x è la distanza dalla linea media, cioè il raggio del tubo più lo spessore del cordone di saldatura a, J e JP rispettivamente il momento d’inerzia e il momento polare, entrambi dipendenti dallo spessore del cordone di saldatura:
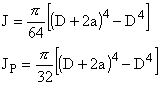
Nelle seguenti tabelle è calcolato il valore minimo del cordone di saldatura; il valore di carico di snervamento Rs è differente a seconda che si consideri l’albero pieno (Rs = 360 MPa) o l’albero cavo (Rs = 250 MPa), il valore di carico limite è pari a Rs diviso 1.5:
|
|
Albero
pieno Fe 510 |
Albero
cavo X5CrNi1810 |
||||||
|
|
D
saldatura = |
110,00 |
mm |
s
eq < 0,7s amm |
D
saldatura = |
139,70 |
mm |
s
eq < 0,7s mm |
|
|
Rs
= |
360,00 |
Mpa |
Rs
= |
250,00 |
Mpa |
||
|
|
s
amm =
|
240,00 |
Mpa |
s
amm =
|
166,67 |
Mpa |
||
|
a
[mm] |
s
^ |
t
|| |
s
eq |
s
^ |
t
|| |
s
eq |
||
|
1,00 |
90,94 |
34,63 |
97,31 |
FALSO |
56,49 |
21,51 |
60,45 |
FALSO |
|
2,00 |
45,04 |
17,15 |
48,20 |
FALSO |
28,04 |
10,68 |
30,00 |
FALSO |
|
3,00 |
29,74 |
11,33 |
31,82 |
FALSO |
18,55 |
7,07 |
19,85 |
FALSO |
|
4,00 |
22,09 |
8,41 |
23,63 |
VERO |
13,81 |
5,26 |
14,78 |
VERO |
|
5,00 |
17,49 |
6,66 |
18,72 |
VERO |
10,96 |
4,17 |
11,73 |
VERO |
|
6,00 |
14,43 |
5,49 |
15,44 |
VERO |
9,06 |
3,45 |
9,70 |
VERO |
|
|
Albero
pieno Fe 510 |
Albero
cavo X5CrNi1810 |
||||||
|
|
D
saldatura = |
110,00 |
mm |
s
eq < 0,7s amm |
D
saldatura = |
139,70 |
mm |
s
eq < 0,7s mm |
|
|
Rs
= |
360,00 |
Mpa |
Rs
= |
250,00 |
Mpa |
||
|
|
s
amm =
|
240,00 |
Mpa |
s
amm =
|
166,67 |
Mpa |
||
|
a
[mm] |
s
^ |
t
|| |
s
eq |
s
^ |
t
|| |
s
eq |
||
|
1,00 |
128,39 |
48,89 |
137,38 |
FALSO |
79,76 |
30,37 |
85,35 |
FALSO |
|
2,00 |
63,59 |
24,22 |
68,05 |
FALSO |
39,59 |
15,07 |
42,36 |
FALSO |
|
3,00 |
41,99 |
15,99 |
44,93 |
FALSO |
26,19 |
9,97 |
28,03 |
FALSO |
|
4,00 |
31,18 |
11,87 |
33,36 |
FALSO |
19,49 |
7,42 |
20,86 |
FALSO |
|
5,00 |
24,69 |
9,40 |
26,42 |
FALSO |
15,48 |
5,89 |
16,56 |
VERO |
|
6,00 |
20,37 |
7,76 |
21,80 |
VERO |
12,79 |
4,87 |
13,69 |
VERO |
Dimensionamento dei cuscinetti
Per impedire spostamento assiale e radiale dell’albero, si montano due cuscinetti a sfere, uno a distanza 100 mm e l’altro 590 mm dalla puleggia condotta.
I cuscinetti andranno poi bloccati con ghiere che ne impediscano la fuoriuscita quando l’albero ruota. E’ preferibile usare ghiere piuttosto che anelli elastici, in quanto questi ultimi per essere montati hanno bisogno di sedi, che rappresentano un intaglio e quindi il pericolo di formazione di microcricche, le quali sarebbero molto gravose e provocherebbero un alto rischio di rottura per fatica.
Il cuscinetto più vicino alla puleggia deve avere un piccolo gioco assiale che permetta un piccolo spostamento. Quindi non deve essere forzato tra lo spallamento e la ghiera.
In base alla casa costruttrice SKF, si scelgono i cuscinetti basandosi sul carico applicato, sul diametro dell’albero nel punto in cui verrà montato il cuscinetto, sul diametro minimo e massimo dello spallamento.
Il diametro dell’albero nella zona in cui andranno montati i cuscinetti dipenderà anche dal diametro interno di questi, valore imposto dalla casa costruttrice.
Sono riportate di seguito le caratteristiche dei cuscinetti scelti, oltre che i relativi valori di diametro dell’albero pieno; per facilitare un eventuale ciclo di lavorazione necessario all’esecuzione del miscelatore tramite lavorazione alle macchine utensili, si è ritenuto opportuno distinguere i vari spallamenti di 5 mm per diametro.
|
|
LIQUIDO A |
LIQUIDO B |
|
Ghiera di bloccaggio puleggia |
D int = M72x2 D est = 110 mm L = 15.3 mm |
D int = M85x2 D est = 98 mm L = 17.3 mm |
|
Sezione minima |
D min = 75 mm L = 60 mm |
D min = 85 mm L = 60 mm |
|
Sezione spallamento |
D = 80 mm L = 69.7 mm |
D = 90 mm L = 65.5 mm |
|
Ghiera di bloccaggio primo cuscinetto |
D int = M85x2 D est = 115 mm L = 17.3 mm |
D int = M95x2 D est = 125 mm L = 18.5 mm |
|
Primo cuscinetto |
D = 90 mm L = 13 mm |
D = 100 mm L = 16 mm |
|
Sezione spallamento |
D = 95 mm L = 425.5 mm |
D = 105 mm L = 454.5 mm |
|
Ghiera di bloccaggio secondo cuscinetto |
D = M100x2 L = 19.5 mm |
D = M110x2 L = 19.5 mm |
|
Secondo cuscinetto |
D = 105 mm L = 18 mm |
D = 120 mm L = 16 mm |
|
Sezione spallamento |
D = 110 mm L = 34.7 mm |
D = 125 mm L = 32.7 mm |
In corrispondenza dei due cuscinetti si hanno i seguenti valori di carico applicato:
|
LIQUIDO A |
LIQUIDO B |
|
Carico primo cuscinetto =
1800 N Carico secondo cuscinetto =
1800 N |
Carico primo cuscinetto =
2500 N Carico secondo cuscinetto =
2500 N |
Sono di seguito riportate le caratteristiche dei cuscinetti scelti, quindi le dimensioni di ingombro, le dimensioni minime delle parti che li accolgono e il carico limite sopportato; si può notare che tutte le condizioni sono verificate:
|
|
LIQUIDO A |
LIQUIDO B |
||
|
Primo cuscinetto |
Secondo cuscinetto |
Primo cuscinetto |
Secondo cuscinetto |
|
|
D int [mm] |
90 |
105 |
100 |
120 |
|
D est [mm] |
115 |
160 |
150 |
150 |
|
Larghezza [mm] |
13 |
18 |
16 |
16 |
|
Carico limite [N] |
2800 |
3200 |
3050 |
3500 |
|
D spall min [mm] |
95 |
110 |
105 |
125 |
|
D spall max [mm] |
110 |
155 |
145 |
145 |
Verifica della saldatura sulle palette
Le palette sono di
dimensione rettangolare, di dimensioni pari a l = 500 mm, h = 100 mm
e s = 20 mm. Su di esse agisce un carico P nella direzione
laterale e un carico 0.2P nella direzione superiore, ma si considerano i
mementi flettente e torcente massimi; è possibile applicare le seguenti
relazioni:
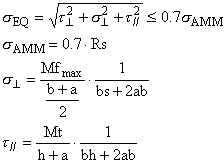
dove a è il
valore di spessore del cordone di saldatura.
A seconda del tipo di fluido si ha sempre un valore minimo del cordone di saldatura di 6 mm.
![]()