Corso
di Laurea in Ingegneria Meccanica
|
ANALISI FEMAl fine di effettuare una
verifica di resistenza per
il nostro impianto frenante, abbiamo deciso di testare le parti
più sollecitate
dal punto di vista meccanico, ossia il gruppo costituito dalle due
semipinze e
dai distanziali. L’intera parte è stata considerata come se
fosse un pezzo
unico, dunque tutti i vincoli sono stati considerati come rigidi.
 Per fare questa verifica di resistenza è stato utilizzato il software CAE Ansys v11. Alcuni problemi si sono verificati nell’importazione del solido: per questioni di licenza, infatti, Ansys non ha importato la geometria di Catia V5, ma è stato necessario risalvare il modello in versione Catia V4 utilizzando il formato .model. Una volta importato il
componente si è passati dunque
alla creazione della mesh. Quest’ultima è stata creata con un
metodo
semi-automatico definito in Ansys e ottimizzato per analisi di tipo
meccanico-strutturali. Non è stato possibile creare una mesh
puramente
tetraedrica con questo software poiché dava alcuni problemi
nella sua
generazione (diversamente da quanto avveniva con altri programmi come
Catia o
MSC Patran).
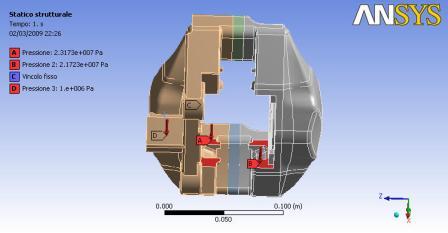
 Il lavoro di “meshatura” non si è tuttavia ancora concluso: è stato fatto un’ affinamento della griglia fino a tre volte nelle zone considerate più gravose: queste in particolare sono i fori che andranno ad accoppiarsi con il porta mozzo. 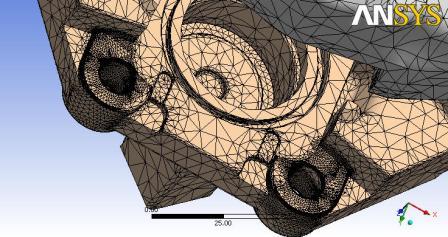 Terminata la creazione della mesh si è passati alla definizione dei carichi e dei vincoli. Per eseguire una corretta analisi sono stati naturalmente considerati dei valori massimali di carichi esercitati sul gruppo. Un
primo carico è stato individuato nella pressione dell’olio pari
a 50 bar, che
agisce all’interno della sede del pistoncino. Un secondo carico
risulta essere quello scaricato dalle
pastiglie a causa della forza frenante. Questo carico è stato
ricavato dapprima
trovando la forza normale esercitata dalle pastiglie sul disco (uguale
al
prodotto tra pressione nell’impianto idraulico e area di base dei
pistoncini),
moltiplicando poi questa per un opportuno coefficiente d’attrito (nel
nostro
caso è stato ragionevole ipotizzare 0,4) e dividendo infine la
forza
tangenziale per l’area di appoggio della pastiglia sulla singola pinza
(ipotizzando pressioni costanti). Eseguendo questi calcoli sono stati
trovati i
valori di pressione pari a 11,5867 MPa per l’area di appoggio sulla
semipinza
con orecchie e 10.8615 MPa per la semipinza senza orecchie.
Per
la definizione dei vincoli nelle due sedi per i portamozzi sono infine
state
considerate delle soluzioni apposite per simulare una cerniera. E’
stato
infatti definito un vincolo di spostamento traslazionale dato da un
vettore
<0,0,0> e un vincolo rotazionale dato dal vettore <0,0, >,
applicato al luogo dei punti interni ai due fori. In questo modo sono
stati
infatti bloccati tutti i gradi di libertà, ad eccezione di
quello attorno
all’asse di rotazione della cerniera. E’ opportuno segnalare che il
vincolo non
risulta essere perfettamente modellato, poiché viene visto dal
programma come
un vincolo bilatero e non come un semplice appoggio della superficie
sul
portamozzo.  Definiti i carichi e i vincoli è stato possibile ricavare lo sforzo equivalente di Von Mises e l’andamento delle deformazioni. Essendo un componente
meccanico progettato senza
l’ausilio degli elementi finiti, possiamo notare come alcune zone
risultino
chiaramente sovradimensionate, mentre nelle zone in prossimità
delle cerniere
gli sforzi si alzano di molto, raggiungendo il valore massimo pari a
201,99
MPa. Questo poiché in prossimità delle cerniere sono
stati trovati, già in fase
di progettazione, i valori di sforzo massimo utilizzando dei modelli
analitici
  Un’ultima analisi è stata effettuata inserendo in Ansys i dati relativi alla nostra lega di alluminio. In particolare sono stati inseriti il Modulo Elastico, pari a 72000 MPa, il coefficiente di Poisson di 0.34, il carico di rottura di 280 MPa e il carico di snervamento di 240 MPa. Grazie a questi dati è stato possibile tracciare la mappatura dei coefficienti di sicurezza. 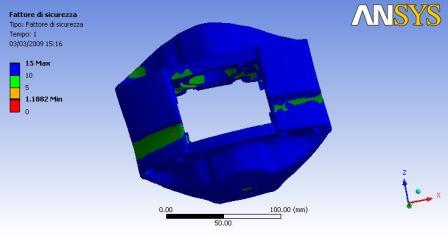 Osserviamo
che il minimo coefficiente di sicurezza risulta essere pari a 1.19,
valore
piuttosto basso ma riferito a un massimale assoluto di carico. In
secondo luogo
osserviamo che questo valore si verifica solamente in corrispondenza di
un
piccolo punto intorno alla cerniera, in tutto il resto della pinza i
valori
sono decisamente superiori, spesso compresi tra 10 e 15. Possiamo
inoltre
riscontrare che questo valore può essere assunto per la non
perfetta
modellazione del vincolo di cerniera, il programma assume infatti
questo
vincolo come bilatero anziché monolatero, come dovrebbe essere
un vero
appoggio.
 |