Aspetto che ci è sembrato particolarmente interessante approfondire nel nostro progetto è quello della verifica di resistenza a fatica utilizzando interamente un calcolatore. Questo tipo di verifica è costituito da una parte “matematica” e da una parte, diversamente da un’analisi puramente statica, integrata con considerazioni di origine sperimentale. Per fare ciò sono state quindi sfruttate le librerie presenti nel software CAE utilizzato, Ansys v11.

Il punto di partenza di questa analisi a fatica è stato proprio il risultato dell’analisi statica precedentemente menzionata. Grazie all’analisi statica sono stati infatti ricavati i tensori dello sforzo nei momenti di massima sollecitazione.

Successivamente si è scelto il tipo di analisi a fatica da effettuare. La scelta è stata tra un modello “S-N”, stress-number of cycles, e “E-N”, strain-number of cycles. Tra i due modelli si è optato per quello “sforzi-numero di cicli” poiché è quello da noi maggiormente conosciuto e approfondito nei corsi di “Costruzione di Macchine”.

Lo step seguente è stato la scelta del tipo di carico variabile nel tempo da applicare alla pinza freno. Per motivi di semplicità si è optato per un ciclo di carico di tipo sinusoidale ad ampiezza costante. Questa scelta non è stata fatta per una vera e propria “convinzione”, infatti esisterebbero alcuni cicli di carico  studiati statisticamente, di forma decisamente piu complessa, studiati appositamente per il campo automotive. Questi cicli di carico si trovano, ad esempio, nelle librerie dei programmi MSC, che non abbiamo tuttavia potuto utilizzare per problemi di licenza.

Il tipo di carico utilizzato sarà naturalmente un tipo di carico a “base zero”, ossia un carico che assumerà come valore inferiore proprio lo zero. Riportiamo i coefficienti moltiplicativi del carico massimo, ossia la nostra curva di carico  normalizzata rispetto all’intensità massima.

Terminata l’assegnazione dei cicli di carico, avendo uno sforzo medio diverso da zero, si è scelto il tipo di diagramma di Haigh da utilizzare, ossia si è dovuta scegliere l’influenza dello sforzo medio sulla resistenza globale. Le diverse opzioni sono state quella di Goodman, di Soderberg, di Gerber, oppure quella di trascurare interamente l’effetto dello sforzo medio. L’ipotesi scelta è quella di Goodman poiché si tratta di quella più comunemente utilizzata.

Infine, per tenere in considerazione i parametri b₂ b₃ e K_f, si è dovuto inserire nel programma il tipo di lavorazione subita dal componente ed eventuali trattamenti superficiali. Come processo tecnologico è stato indicato la fonderia, infatti la pinza proviene quasi interamente da una colata in conchiglia (salvo pochissime superfici lavorate per fresatura o foratura di importanza trascurabile). Infine non è stato indicato alcun trattamento superficiale, non avendo subito trattamenti che migliorano la resistenza a fatica come pallinatura, nitrurazione, cementazione. Unendo queste informazioni alla conoscenza del gradiente degli sforzi (calcolato nella precedente soluzione statica), il sistema è in grado di stimare i tre parametri mancanti.

Siamo riusciti in questo modo a metterci nel caso di una sollecitazione monoassiale, con sforzo medio nullo, su un provino non intagliato, di diametro al più 10 mm e “lucidato a specchio”.

Abbiamo infine a disposizione, dalle librerie di Ansys, una curva di Wohler per una lega di alluminio che ben approssima quella della lega BDS-06.01.

Con quest’ultimo elemento possiamo dunque effettuare un’analisi di resistenza a fatica, assumendo come valore limite per la cosiddetta “vita infinita” 10⁸ cicli, valore comunemente utilizzato per le leghe di alluminio (anche se l’alluminio non ammette un vero e proprio limite di fatica, avendo una struttura cristallina CFC).

Grazie al software utilizzato è stato possibile mappare la vita espressa in numero di cicli per tutto il pezzo.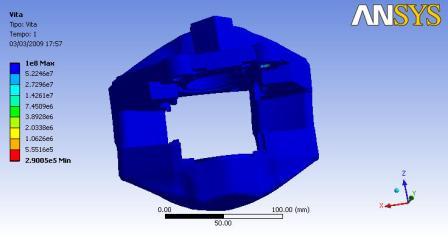

Come vediamo l’intera pinza freno resiste a fatica per oltre 10⁸ cicli, salvo un piccolo punto all’interno della cerniera dove la vita del componente assume il valore minimo di 290000 cicli. Ciò si verifica in primo luogo poiché la verifica di resistenza è stata effettuata imponendo un’ampiezza di carico costante pari al massimale, in secondo luogo per la non perfetta modellazione del vincolo di appoggio, visto come un vincolo bilatero dal programma anziché monolatero come sarebbe corretto auspicarsi.

Riportiamo infine la distribuzione della sollecitazione alternata equivalente. Come lecito prevedere questa risulta essere sotto il limite di fatica in tutti i punti del solido, salvo nel solito punto interno alla cerniera per i motivi prima citati.