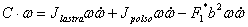| |
| .:Home:. .:Analisi funzionale, obiettivi e vincoli:. .:Giunti:. .:Modellazione della struttura:. .:Analisi FEM:. .:Rendering:. .:Credits:. .:Bibliografia:. | |
|
MODELLIZZAZIONE DEL PROBLEMA
Dopo l'analisi dell'esistente si sono calcolate le forze e le coppie agenti sul sistema, attraverso equilibri dinamici per calcolare il momento torcente massimo sull'albero del polso. 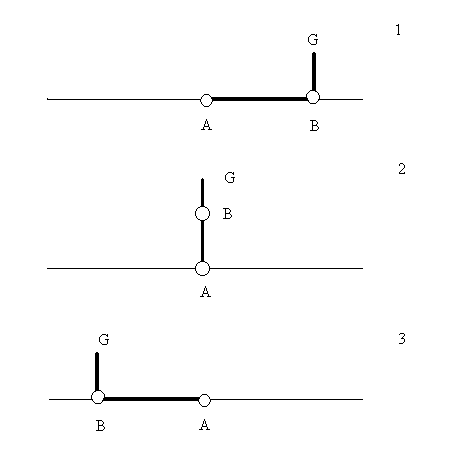 Dove AB è l'interasse del braccio (1167,5 mm ) e BG distanza tra baricentro della lastra e estremo del braccio (154mm). Per facilitare il calcolo delle inerzie in gioco si è pensato di concentrare la massa del polso (≈75 kg) nel punto B (cosa effettivamente fattibile come evidenzia l'analisi della distribuzione delle masse del polso), mentre G rappresenta il baricentro della lastra ( massa max 150 kg). Per calcolare le inerzie in gioco si è pensato alla configurazione 3, ovvero in frenata, andando a calcolare la lunghezza AG. A questo punto si mettono le inerzie collegate alle masse, secondo il seguente schema: 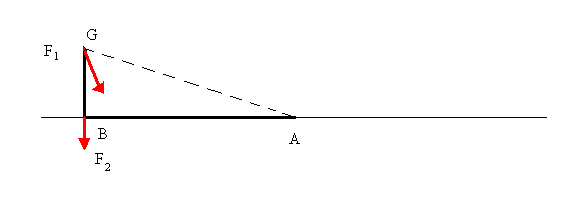 Dove: 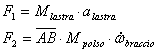 Per le inerzie dovute alla rotazione abbiamo schematizzato in questo modo: 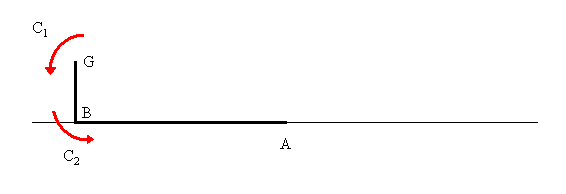 Dove: 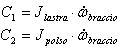 Adesso non resta che scrivere l'equazione di equilibrio di potenza per il motore che permette al polso di rimanere in posizione, ipotizzando che velocità e accelerazioni siano uguali in modulo, ma in verso opposte a quelle del motore che movimenta il braccio: 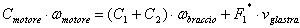 , ,dove F asterisco è la componente di F1 normale a GB. Adesso è necessario introdurre i legami cinematici sulle velocità e accelerazioni angolari. 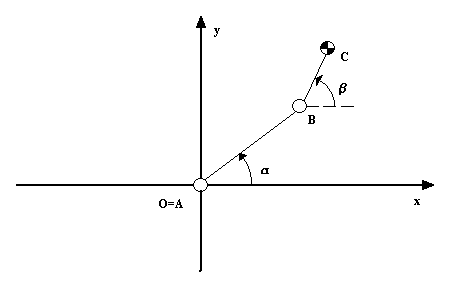 Preso come origine del sistema di riferimento il punto A si possono scrivere le equazioni delle componenti di G rispetto a A: 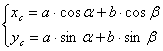 A questo punto calcolo le componenti della velocità derivando il sistema rispetto al tempo: 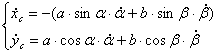 Derivando ulteriormente si ottengono le componenti dell'accelerazione: 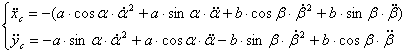 Adesso per ottenere i valori numerici che mi servono devo applicare i dati che derivano dal caso studiato, ovvero: 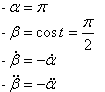
Calcolate accelerazioni e velocità di G, la nostra equazione per calcolare il momento torcente diventa: 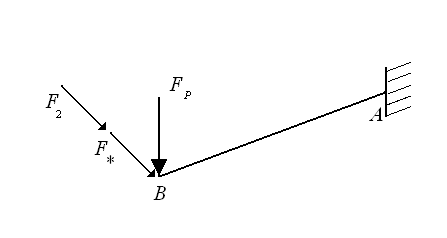 Dove Fp è pari alla massa del polso più quella della lastra moltiplicate per l'accelerazione di gravità, mentre F* è la componente normale a AB della forza F1 e, infine, F2 è la forza d'inerzia associata alla massa del polso. Per quanto riguarda i momenti, invece, abbiamo una sola componente:dovuta al momento di trasporto dovuto allo spostamento della forza peso della lastra, pari, quindi a 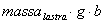 . .Direzione e verso del momento sono evidenziati nella seguente figura: 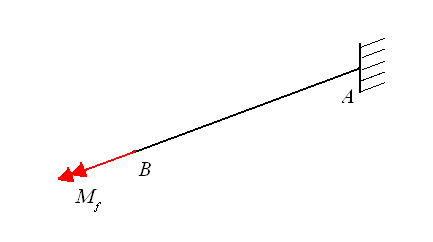 Altro componente sottoposto a uno stato di sforzo particolare è l'albero di attacco del polso. Sempre rifacendosi a costruzione di macchine lo si è modellato come una trave in cui i due cuscinetti presenti vengono cambiati nei vincoli di cerniera e carrello secondo lo schema rappresentato nella seguente figura: 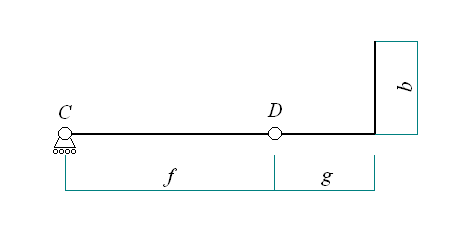 Dove b= 154 mm, g = 438 mm e f = 90 mm. Su tale albero agiscono le forze peso della lastra e del polso, nonché la forza d'inerzia associata alla massa della lastra, secondo il seguente schema: 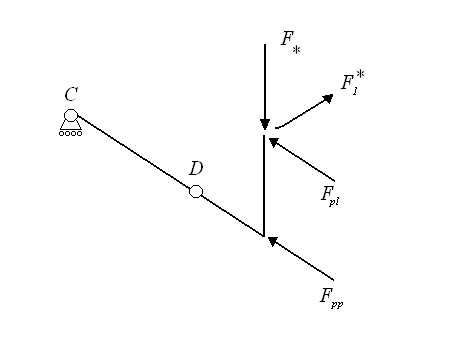 Dove F* è la componente della forza d'inerzia normale alla direzione CD e  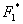 la componente della forza d'inerzia utilizzata per il calcolo della coppia resistente. la componente della forza d'inerzia utilizzata per il calcolo della coppia resistente.Allo schema precedente va aggiunta le coppia d'inerzia Mi calcolata per il modello del braccio: 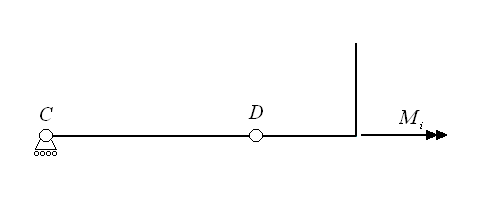 I moduli delle forze e dei momenti trattati in questo capitolo sono disponibili cliccando su questo link: File excel. A partire dalle reazioni calcolate in C e D è stato possibile scegliere, attraverso la procedura guidata nel manuale SKF, i rispettivi cuscinetti. Per il punto C si è scelto un tradizionale cuscinetto a sfere, mentre per il punto D si è optato per un cuscinetto a rulli conici, più adatto a reggere il carico assiale. Da catalogo si è deciso di montare i cuscinetti SKF 32008 X e SKF 61906 per il polso e SKF 61806 altrove. |
|
| Inizio Pagina | |
| © 2008 - Progetto a cura di Paolo Magnoni, Lorenzo Penati, Davide Pozzi e Silvio Rabbolini - Laboratorio Progettuale di Disegno Assistito dal Calcolatore | |
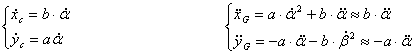
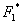 , quindi, risulta particolare, in quanto fornisce potenza positiva al sistema.
, quindi, risulta particolare, in quanto fornisce potenza positiva al sistema.