|
|
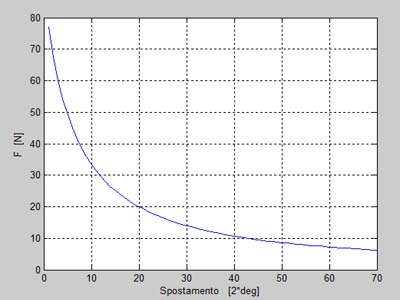 |
Quella diagrammata è la forza minima necessaria per innsescare il movimento, considerando successivi stati di equilibrio.
Di seguito è riportato il programma matlab utilizzato.
l1=17.6/1000;
b=7.75/1000;
alfa=122;
gamma=16;
c=0.4;
k=0.598;
l0=62;
l=16;
f=k*(l0-l);
t=0;
FF=zeros(1,70);
X=1:70;
d=1.75/1000;
for i=0.5:0.5:35
t=t+1;
gamma=gamma+i;
beta=180-alfa-gamma;
...
|
...
for F=0.1:0.1:100
N=(F+f)/(sin(((90-beta)*pi)/180)+c*cos(((90-beta)*pi)/180));
H=N*(cos(((90-beta)*pi)/180)-c*sin(((90-beta)*pi)/180));
M=H*d;
if F*cos(((90-gamma)*pi)/180)*l1>N*c*b+M
break;
end
end
FF(t)=F;
gamma=16;
end
plot(X,FF,'b')
grid on;
xlabel('Spostamento [2*deg]');
ylabel('F [N]');
hold on;
|
|
|
|
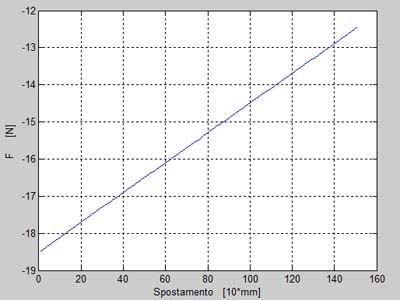 |
Le forze in questa fase sono molto basse poiché secondo la modellizazione utilizzata si ricavano le forze minime necessarie affinchè ci sia movimento, non quelle che realmente applicherebbe l'anta che viene trascinata dalla chiusura.
Di seguito è riportato il programma matlab utilizzato.
l1=18.3/1000;
b=7.75/1000;
delta=16.5;
c=0.4;
t=0;
h=8.5/1000;
l0=62;
l=16;
k=0.598;
FF=zeros(1,151);
X=1:151;
for i=0:0.1:15
t=t+1;
f=k*(l0-(l+i));
...
|
...
for F=100:-0.01:0.01
N=(F*cos(((90-delta)*pi)/180)*l1)/h;
R=N*c;
if f>F+R+N*c
break;
end
end
FF(t)=F;
end
plot(X,-FF,'b')
grid on;
xlabel('Spostamento [10*mm]');
ylabel('F [N]');
hold on; |
|
|
|
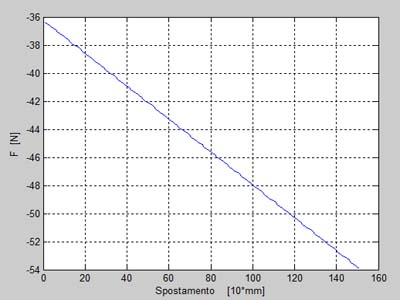 |
La forza in questa fase è quella che determina in maggior parte la forza necessaria all'apertura dell'anta; si può notare che la forza massima è di ~50N, il che corrisponde ai dati sperimentali fornitici dall'azienda produttrice.
Di seguito è riportato il programma matlab utilizzato.
j=0;
col=['b','g','k','r'];
for z=0:1:3
j=j+0.1;
Z=j*ones(151);
co=18.46/1000;
se=(5.2+z)/1000;
l1=((se^2+co^2)^0.5);
delta=atan(se/co);
b=7.75/1000;
c=0.4;
t=0;
h=8.5/1000;
l0=62;
l=16;
k=0.598; %N/mm
FF=zeros(1,151);
X=1:151;
for i=15:-0.1:0
t=t+1;
f=k*(l0-(l+i));
...
|
for F=0.1:0.1:10000
N=(F*sin(delta)*l1)/h;
R=N*c;
if f+R+N*c<F
break;
end
end
FF(t)=F;
end
plot(X,-FF,col(z+1));
grid on;
hold on;
end
xlabel('Spostamento [10*mm]');
ylabel('F [N]');
legend('0mm','1mm','2mm','3mm');
axis([0 160 -130 -20]);
title('Scorrimento in apertura'); |
|
|
|
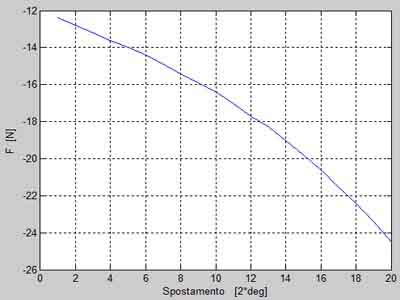 |
Si può notare che questa fase e la sua corrispondente in chiusura hanno influenza minore rispetto alla fase di scorrimento rettilineo in apertura sulla forza totale.
Di seguito è riportato il programma matlab utilizzato.
l1=18.06/1000;
b=7.75/1000;
alfa=152;
gamma=11.2;
c=0.4;
k=0.598;
l0=62;
l=16;
f=k*(l0-l);
t=0;
FF=zeros(1,20);
X=1:20;
d=1.75/1000;
for i=0.5:0.5:10
t=t+1;
gamma=gamma-i;
beta=180-alfa-gamma;
...
|
...
for F=0.001:0.1:100
N=(f-F)/(sin(((90-beta)*pi)/180)+c*cos(((90-beta)*pi)/180));
H=N*(cos(((90-beta)*pi)/180)-c*sin(((90-beta)*pi)/180));
M=H*d;
if F*cos(((90-gamma)*pi)/180)*l1>N*c*b+M
break;
end
end
FF(t)=F;
gamma=11.2;
end
figure();
plot(X,-FF,'b')
grid on;
xlabel('Spostamento [2*deg]');
ylabel('F [N]');
hold on; |
|
Confronto con risultati sperimentali da ROLD
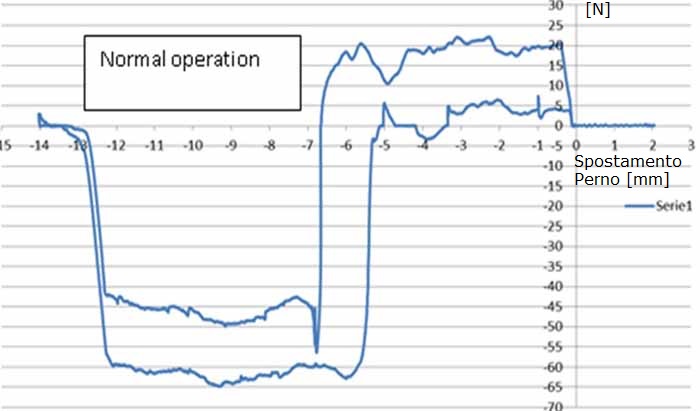
Questo grafico è confrontabile con quelli ottenuti tenendo però conto del segno della F e che le fasi di rotazione hanno rilevanza minore rispetto a quelle di scorrimento. Il fatto principale da notare è che la forza richiesta per l'apertura è circa 60N così come quella che abbiamo ottenuto attraverso la nostra analisi teorica.
-Torna su- |





