Multibody Systems

" I metodi proposti per l'analisi, in genere non lineare, dei sistemi meccanici implementati sui moderni  calcolatori digitali sono attualmente in grado di simulare con grande accuratezza il comportamento statico e dinamico delle macchine e delle strutture sottoposte all'azione dei carichi esterni. Tali metodologie sono basate sul concetto di sostituire il sistema reale con un modello matematico equivalente costituito da un numero discreto di corpi rigidi o deformabili collegati da elementi elastici e dissipativi.

Il modello matematico opportunamente implementato in un programma di calcolo può essere in tal modo utilizzato come prototipo "virtuale" del sistema reale. Un tale approccio al problema E' ormai usualmente adottato per simulare il comportamento dinamico di macchine, meccanismi, veicoli, robot e strutture spaziali.

I modelli matematici sono, con tale approccio, rappresentati da sistemi multicorpo (con dicitura anglosassone Multibody Systems), ciascuno dei quali è genericamente sottoposto a grandi spostamenti e rotazioni nello spazio.

Le equazioni che governano il moto di tali sistemi sono complesse ed altamente non lineari e, nella maggior  parte dei casi, non possono essere risolte analiticamente in forma chiusa. Tali equazioni sono attualmente generate automaticamente e risolte numericamente da codici "General Purpose": il progettista viene così ad essere alleviato dal compito di ricavare personalmente le complesse equazioni di moto e dell'implementazione su calcolatore. "

Tratto dall'introduzione a: G. Diana - F. Cheli: Cinematica e Dinamica dei sistemi multicorpo (pubblicazione sviluppata per i corsi di Modellistica e Simulazione dei Sistemi Meccanici e Meccanica del Veicolo tenuti dagli Autori presso il Politecnico di Milano)

Matrici di Trasformazione

La costruzione di un modello matematico in grado di simulare il comportamento del sistema multicorpo oggetto del presente studio si basa sulla scrittura delle matrici di trasformazione che corrispondono ai giunti del meccanismo. Seguendo la catena di trasformazioni attraverso le corrispondenti matrici è allora possibile controllare gli spostamenti del sistema meccanico. In questo progetto, tutti i corpi presi in considerazione sono stati considerati rigidi e indeformabili.

Il primo passo per la scrittura delle matrici di trasformazione è la comprensione delle matrici di rotazione.
Tali matrici consentono di convertire la rappresentazione del vettore dal sistema di riferimento j (di partenza) al sistema di riferimento i (di arrivo).

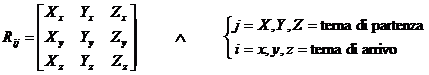
Le colonne della matrice sono composte dai coseni direttori degli assi del sistema  j di partenza (X, Y, Z) rispetto agli assi del sistema i di arrivo (x, y, z). I coseni direttori sono i coseni degli angoli formati da un vettore con gli assi di riferimento.

Rotazione del sistema di riferimento 1 (X,Y,Z) di ϑ attorno a:

Il secondo passo verso la realizzazione delle matrici di trasformazione è costituito dall'introduzione delle coordinate omogenee:

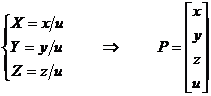
u è il fattore di scala; se 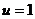 x,y,z sono le coordinate cartesiane; se 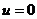 il vettore rappresenta un punto improprio, ovvero una direzione nello spazio.

Siamo ora in grado di descrivere la struttura di una matrice di trasformazione:

      

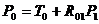
A ogni giunto del robot si associa una matrice di trasformazione che descrive il movimento effettuato. Tale matrice dipenderà da uno o più parametri: l'input della cinematica diretta o l'output di quella indiretta.

Ecco alcuni esempi:

Accoppiamento rotoidale:                   

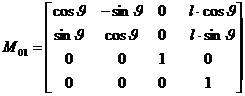
Accoppiamento prismatico:                 

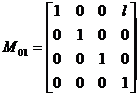
Tramite i metodi della premoltiplicazione e postmoltiplicazione si utilizzano le matrici di trasformazione dei singolo giunti per descrivere l'intera catena cinematica.