


Loop![]()
Fino ad ora abbiamo visto come l'utilizzo combinato di due Haptic Masters possa facilmente garantire alla piattaforma end effector 5 gradi di libertà (DoF), ovvero le tre coordinate della posizione e la rotazione attorno agli assi z e x.
Il cinematismo posto all'estremità
dei due bracci robotici ha lo scopo di conferire all'end effector il
sesto ed ultimo DoF, consentendo la rotazione attorno all'asse y.
Ciò viene garantito attraverso un loop (ciclo chiuso) che lega
l'inclinazione della piattaforma rispetto all'asse y alla distanza tra
le estremità dei due Haptic Masters. Sarà quindi la distanza tra i due
bracci robotici a determinare la posizione finale dell'end effector, che
sarà dotato di tutti i DoF di un corpo libero nello spazio.
N ella
figura seguente viene schematicamente illustrato il funzionamento del
cinematismo con loop:
ella
figura seguente viene schematicamente illustrato il funzionamento del
cinematismo con loop:

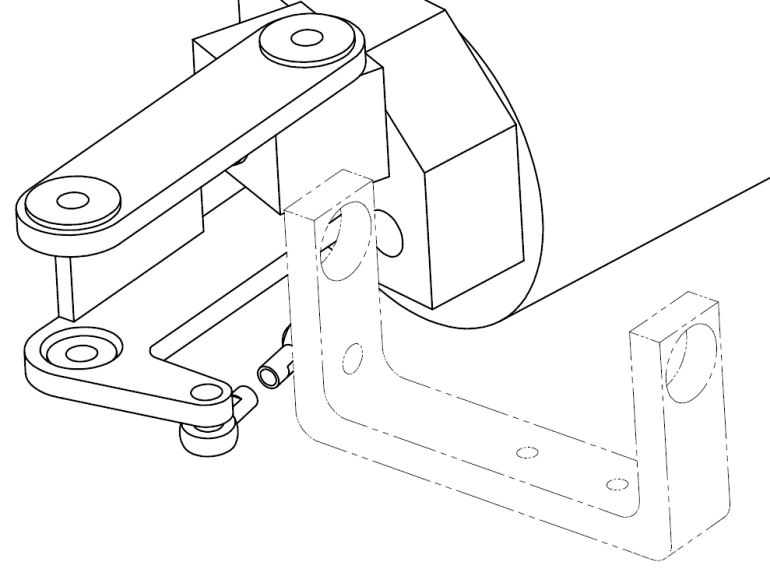
![]() Se
Se  c'è
c'è  un avvicinamento tra le estremità degli Haptic Masters, il componente 1 si avvicina al
componente 2. Affinché in questa situazione venga rispettato il vincolo
imposto dai due giunti sferici collegati (3) - in sostanza la loro
distanza deve rimanere costante - la piattaforma end effector è
costretta a ruotare in senso orario attorno all'asse y; ovviamente un
allontanamento tra i due bracci robotici produrrà l'effetto opposto.
un avvicinamento tra le estremità degli Haptic Masters, il componente 1 si avvicina al
componente 2. Affinché in questa situazione venga rispettato il vincolo
imposto dai due giunti sferici collegati (3) - in sostanza la loro
distanza deve rimanere costante - la piattaforma end effector è
costretta a ruotare in senso orario attorno all'asse y; ovviamente un
allontanamento tra i due bracci robotici produrrà l'effetto opposto.
Come può essere descritto questo cinematismo utilizzando le matrici di trasformazione?
Il nostro problema è Il seguente: nota la posizione e
l'orientazione della terna mobile solidale all'end effector, come
determinare l'angolo α di rotazione dell'end effector attorno
all'asse y di tale terna? Tale angolo è l'unico in grado di rispettare
il vincolo di distanza tra i due giunti sferici sopra evidenziati.
Per loop come questo non è possibile scrivere una soluzione in forma
chiusa. Siamo però in grado di individuare un metodo iterativo che,
sfruttando le capacità computazionali dei calcolatori, permetta di
trovare rapidamente un'approssimazione prossima a piacere a tale angolo.
Verrà di seguito illustrata in maniera estremamente sintetica la procedura seguita per individuare l'algoritmo solutivo del problema.
Nella
figura seguente sono
indicati gli angoli, i pun ti
e le terne di
interesse ai fini del nostro calcolo:
ti
e le terne di
interesse ai fini del nostro calcolo:
La posizion e
e l'orientazione della terna A sono note; in tale sistema di riferimento
è facile determinare la posizione del punto P (sede del primo dei due
giunti sferici collegati).
e
e l'orientazione della terna A sono note; in tale sistema di riferimento
è facile determinare la posizione del punto P (sede del primo dei due
giunti sferici collegati).
Si parte con un α di tentativo qualsiasi e si scrive la matrice di
rotazione di tale angolo in senso orario attorno all'asse y. Si scrive
poi la matrice di traslazione che collega la terna A e la terna D (in
pratica tale traslazione è data dalle dimensioni del componente 1
evidenziato nella prima figura di questa pagina). Con queste due matrici
si premoltiplicano le coordinate del punto P, ottenendo infine la sua
posizione rispetto alla terna D.
Rispetto alla terna D è facile determinare la posizione del punto R, che
sarà ruotato di un certo angolo δ per mantenere costante la lunghezza
del segmento RP. Tale lunghezza è nota, ed è proprio essa che si va a
imporre per risalire all'angolo δ a partire dall'α iniziale di
tentativo.
Noti gli angoli α e δ in questa situazione e le dimensioni del pezzo 2,
è facile risalire alla terna posta alla sua base. A questo punto,
considerando per semplicità tale terna posta esattamente al termine
dell'Haptic Master, si verifica che il suo asse z sia perpendicolare al
braccio robotico. Tale verifica viene eseguita con il prodotto scalare:
se esso è maggiore di un ε piccolo a piacere, il ciclo si ripete con un
piccolo incremento di α.
Ovviamente piccoli incrementi di α rallenteranno il ciclo ma
consentiranno una migliore precisione.
Il ciclo verrà poi ripetuto decrementando α, e alla fine verrà scelto
l'angolo minore in modulo.
Per qualsiasi chiarimento e per l'analisi dettagliata della routine in
MATLAB, si rimanda all'esposizione orale del progetto.