Dinamica
Dopo aver analizzato attentamente l'aspetto cinematico del problema possiamo passare ad occuparci di quello dinamico andando a calcolare le forze agenti sul nostro sistema.
L'ing. Baiardo, nel primo colloquio, ci ha fornito le forze e i momenti principali che agiscono sullo snodo preso in considerazione:
| Momento: M3 | 18 800 000 Kg mm = 180 000 Nm |
| Forza verticale: T3 | 2300 Kg = 23000 N |
Questi dati sono approssimati per eccesso e possono essere considerati costanti per qualsiasi configurazione del sistema, infatti è sempre possibile posizionare gli stadi successivi in modo da generare tali valori. In particolare questi rappresentano le sollecitazioni indotte dal peso, dal movimento e dalle forze dei bracci numero 4 e 5 che sono collegati in serie al braccio numero 3.
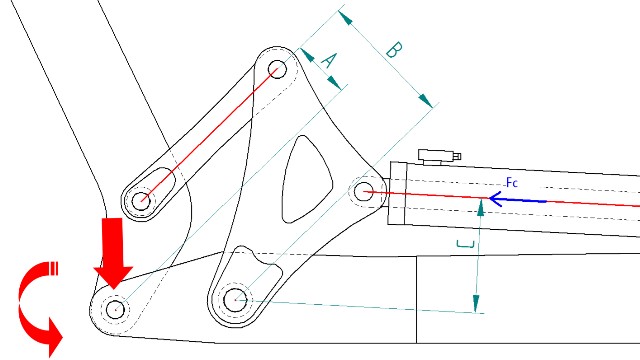
Nella figura seguente sono rappresentate in maniera schematica le forze applicate allo snodo e alcune dimensioni principali del cinematismo, che ci serviranno per lo studio della dinamica:

Ora il nostro scopo è quello di riuscire a calcolare in che modo si modifica la forza Fc agente sullo stantuffo a seconda della variazione delle dimensioni A, B, C che governano l'intero meccanismo; in questo modo sarà possibile effettuare delle analisi di resistenza nelle zone più sollecitate. Introducendo vecchie conoscenze di meccanica razionale, possiamo scrivere le seguenti relazioni:
Equilibrio alla rotazione rispetto allo snodo Braccio 2 - Braccio 3:
|
Fb=Mf/A |
dove Mf è il momento flettente imposto;
Momento flettente agente sullo snodo per l'equilibrio alla rotazione della forcella rispetto a P3:
|
Fb x B = Fc x C |
sostituendo a Fb il valore sopra ricavato si ha:
|
(Mf x B)/A = Fc x C |
Otteniamo quindi:
|
Fc = (Mf x B)/(A x B) |
A questo punto possiamo passare ad analizzare le forze in gioco nella configurazione standard:
| Forze nella configurazione standard |