|
|
|
|
|
|
|
|
|
PORTATA
PINZA[kg]
|
2200
|
3200
|
4200
|
SPINTA
ASSIALE[kN]
|
100
|
125
|
180
|
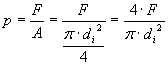
PORTATA
PINZA[kg]
|
2200
|
3200
|
4200
|
DIAMETRO
INTERNO[mm]
|
96
|
107
|
128
|
SPINTE
ASSIALI OTTENIBILI[kN]
|
101
|
126
|
180
|
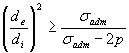
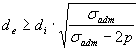
P
|
2200
|
3200
|
4200
|
DIAMETRO ESTERNO[mm] |
110
|
122
|
146
|
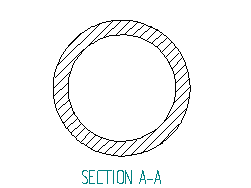 La normativa mi permette di conoscere la sezione più sollecitata ,che è
all’intradosso ,dove ho la presenza delle seguenti sollecitazioni (la cui
espressione è per l’appunto ricavata dalle norme sui tubi assial-simmetrici)
La normativa mi permette di conoscere la sezione più sollecitata ,che è
all’intradosso ,dove ho la presenza delle seguenti sollecitazioni (la cui
espressione è per l’appunto ricavata dalle norme sui tubi assial-simmetrici)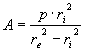
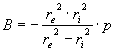
MODELLO
PINZA
|
Ri
|
Re
|
st
|
sconfr
|
2200
|
48
|
55
|
103
|
58,5
|
3200
|
53,5
|
61
|
107,3
|
60,65
|
4200
|
64
|
73
|
107
|
60,5
|
MODELLO
PINZA
|
sconfr
|
2200
|
110
|
3200
|
114,9
|
4200
|
114,6
|
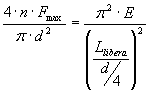
PORTATA
PINZA[kg]
|
2200
|
3200
|
4200
|
DIAMETRO
STELO[mm]
|
36
|
39
|
42
|