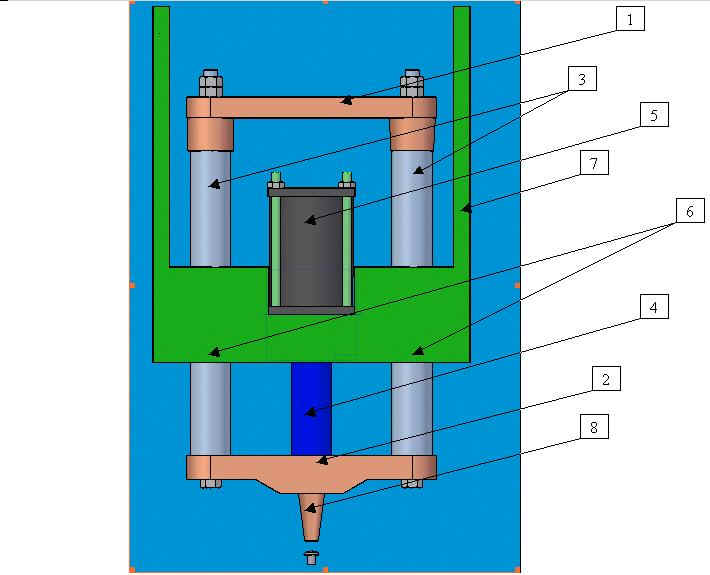
Analisi inflessione e resistenza
Conclusioni e considerazioni finali
Vai alla home page

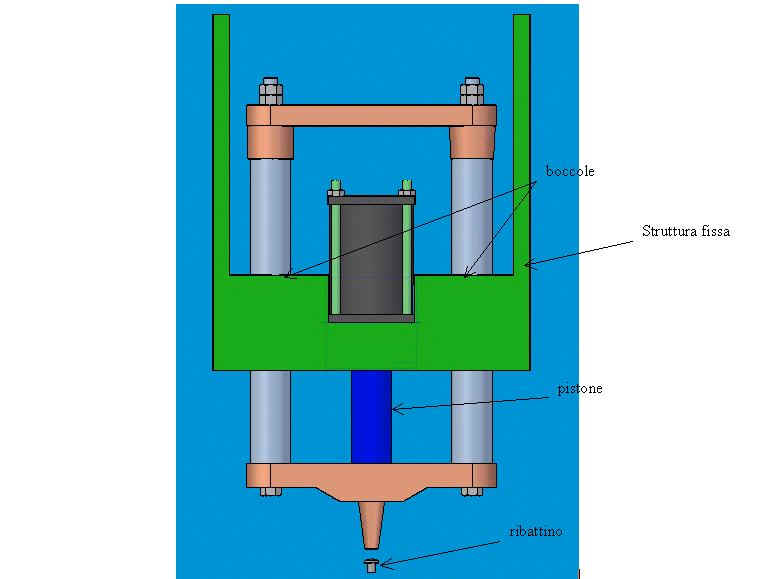
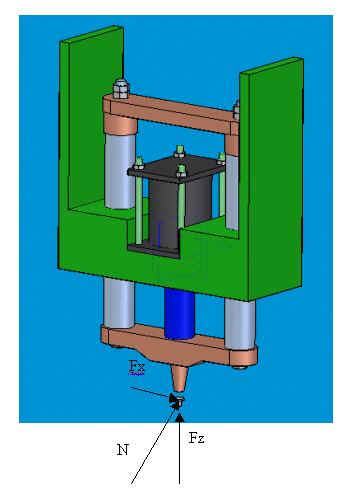
1. traversa di collegamento tra gli estremi delle colonne superiore
2. traversa di collegamento tra gli estremi delle colonne inferiore
3. colonne
4. pistone oleodinamico
5. cilindro oleodinamico
6. boccole sedi delle colonne
7. supporto o base
8. punzone di ribattituraDurante la ribattitura la forza verticale che agisce sul ribattino è data dall’azione del pistone posto tra le colonne;la forza viene trasmessa al ribattino dal punzone di ribattitura. Le colonne scorrono all’interno delle boccole.
Problema (malfunzionamento)
La rivettatrice in questione può essere soggetta a malfunzionamenti dovuti all’inclinazione a cui il rivetto è soggetto quando non è perfettamente centrato nel foro delle lamiere. Questo inconveniente determina un’inflessione delle colonne. Nostro compito è appunto quello di valutare se tale inflessione compromette o no il funzionamento e l’integrità della macchina. Occorre distinguere tra due diverse inflessioni delle colonne, infatti il rivetto si può inclinare sia trasversalmente che longitudinalmente. Ovviamente un’inclinazione trasversale del rivetto implica un’inflessione in avanti delle colonne, così come un’inclinazione longitudinale implica un’inflessione laterale delle colonne.
DESCRIZIONE STRUTTURA IN OGGETTO
Osservazioni e commenti sul programma di modellazione CAD
DESCRIZIONE struttura in oggetto
Per effettuare l’analisi ad elementi finiti della struttura è necessario prima creare l’assieme.
La struttura in oggetto si compone di :
- due colonne
- un supporto o base con due boccole sedi delle colonne
- due traverse di collegamento tra gli estremi delle colonne
- un cilindro oleodinamico
- un pistone oleodinamico
- due viti M14
- due dadi M16
I dati geometrici relativi ai componenti in parte sono stati forniti direttamente dalla Capmac in parte sono stati ricavati dal disegno Autocad fornitoci tramite una amplificazione di scala.Ovviamente l’attendibilità dei dati è doppiamente compromessa in quanto non si è certi che il disegno sia in scala e che i dati inviati dalla Capmac siano reali. D’altra parte non è stato possibile avere i dati geometrici reali per motivi di sicurezza nei confronti della concorrenza.In particolare il pistone ed il cilindro non sono presenti nello schema fornitoci quindi ne abbiamo inventato i dati. d’altra parte nelle ipotesi del modello da noi studiato la loro presenza è completamente inutile in quanto non hanno alcuna influenza sulla flessione e sul carico gravante sulle colonne. La spiegazione accurata è fornita nel capitolo 2.
I programmi di modellazione solida a nostra disposizione sono Solid Edge V14 ed Autodesk Inventor versione 5.1.
Per la scelta del software abbiamo tenuto conto dei seguenti criteri:
Autodesk Inventor (versioni dalla 5.1 in poi) è particolarmente indicato per la realizzazione di assemblies molto complessi data la facile gestione dell’ambiente assembly. Invece il limite del programma è l’ambiente di sketch che risulta meno maneggevole del rispettivo in Solid Edge.
Solid
Edge V14 ha una discreta
gestione degli assiemi ed una ottima facilità di modellazione dei
componenti. Quindi è indicato per la creazione di componenti caratterizzati
da sketch molto complessi.
La parametrizzazione risulta molto più facile in Solid Edge in quanto è particolarmente agevole inserire sia tra i di diversi componenti sia tra le caselle di un foglio Excel e la tabella variables
Il criterio di scelta è stato l’uso della parametrizzazione. Si è ritenuto necessario parametrizzare le dimensioni delle parti linkandole ad un tabella Excel in modo tale da generare un assieme variabile in funzione dei dati inseriti nella tabella. I principali motivi di tale scelta sono due:
1) ottenere una macchina le cui dimensioni possono essere variate senza dover entrare nell’ambiente CAD quindi di agevole utilizzo anche per chi non è ‘addetto ai lavori ’.
2) vantaggi per sviluppi futuri della macchina: per verificare la resistenza e la flessione delle colonne dopo aver modificato la dimensione dei part è sufficiente variare i valori nella tabella excell, aprire l’assembly, salvare in formato iges, importare l’assieme o la parte nel programma di analisi elementi finiti. Come si nota i tempi per eseguire tali operazioni sono particolarmente ridotti e nettamente minori rispetto ad un analisi numerica della struttura.
I parametri vincolati al foglio Excel sono solo quelli che si ipotizzano influire sulla flessione delle colonne, sulla rigidità della struttura e sulla resistenza statica.
Abbiamo modellato direttamente i componenti le cui dimensioni erano note (fornite o ricavate dallo schema). Per quanto riguarda cilindro oleodinamico e pistone si è ritenuto opportuno modellarli direttamente nell'ambiente assembly dopo aver realizzato l'assieme parziale dei componenti noti.
Riassumendo prima abbiamo realizzato un
insieme del tipo ‘BOTTOM UP’ dei componenti già realizzati:base, colonne,
traversa_up, traversa_down. Poi abbiamo ‘creato in place’ il cilindro.In
particolare abbiamo adottato degli espedienti per velocizzare la modellazione:
-la creazione di una parte nell’assieme , ‘create in place’
-l’inter-part copy
Quindi si può affermare che l’assembly è stato realizzato parte secondo l’approccio BOTTOM - UP parte secondo la modalità TOP - DOWN in cui:
BOTTOM - UP: realizzazione dell'assemblaggio in gruppi e sottogruppi delle parti già create in ambito 'part'
TOP - DOWN: costruzione di un componente i ambiente assembly sfruttando le relazioni con le altre parti
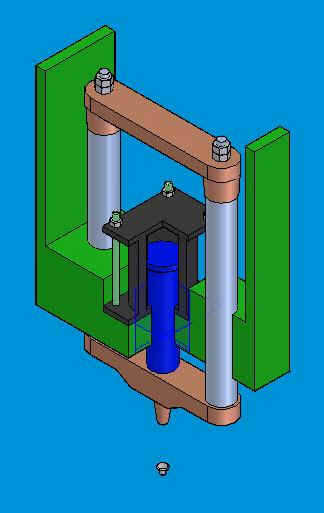
Riportiamo ora l'immagine dell'assieme in cutaway view al fine di visualizzare tutti i componenti modellati:
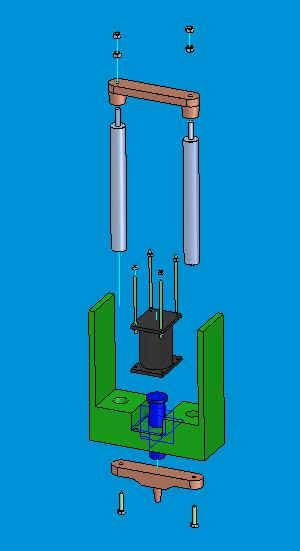
Come descrizione schematica dell'assemblaggio della struttura si riporta l'esploso dell'assieme realizzato.
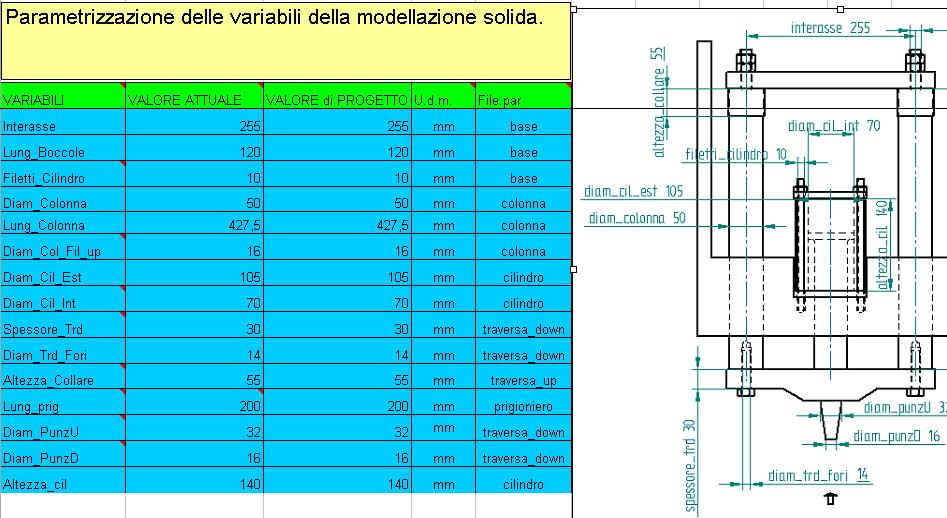
Per avere una gestione delle variabili
indipendenti dell’insieme più agevole ed intuitivamente semplificata, è
stata creata una tabella Excel contenete i parametri di controllo. Si definisce
variabile di controllo o indipendente una variabile il cui valore non è
funzione delle altre variabili del sistema. In generale tutti gli altri
parametri dipendono dal gruppo di variabili indipendenti scelte o in modo
diretto o tramite relazioni matematiche. Quindi si collega il contenuto delle
caselle della tabella Excel alle
righe delle tabelle ‘variables’ dei
singoli part relative alla variabile considerata.
I parametri indipendenti sono:
Osservazioni e commenti sul programma di modellazione CAD
Come anticipato nel paragrafo relativo alla scelta del software, ‘Solid Edge V14’ è particolarmente adatto per la modellazione parametrica di componenti anche geometricamente complesse. Inoltre ha la possibilità di ‘linkare’ il valore dei parametri oltre che a variabili di part diverse anche a tabelle excel. In fase di modellazione è stata di grande utilità la modellazione in ‘place’ (specialmente nel caso di componenti non quotate dimensionalmente) che consente di esaminare direttamente la congruenza della parte nell’insieme.Una nota negativa da segnalare consiste nel fatto che il programma non inserisce il diametro dei fori filettati ( in riferimento alla feature ‘Hole’) nella tabella ‘variables’. Per questo motivo non è stato possibile inserire il diametro delle viti di fissaggio della traversa inferiore sulle colonne come variabile. Un'altra limitazione è l'impossibilità di inserire il link ad un altro file all'interno di una formula.
ANALISI COSTRUZIONE DI MACCHINE
CASO FORZA ORIZZONTALE DIRETTA LUNGO ASSE Y: Fy
FORZA ORIZZONTALE DIRETTA LUNGO ASSE X : FX
Dati fornitici:
- Valori possibili di forza del pistone sulla traversa Fp
- discretizzazione degli angoli di inclinazione dell’asse del ribattino rispetto all’asse z (B).
- dati geometrici della struttura
- dati geometrici del ribattino 8x12 UNI 750
- materiale: acciaoi C45 non temprato (indicazione generica per motivi di sicurezza)
Ipotesi dell’analisi:
-
La struttura della macchina è indeformabile (in verde): corpo rigido
-
boccole indeformabili (o deformazioni trascurabili)
-
gioco nell’ accoppiamento boccola-colonna trascurabile
-
traverse di collegamento delle colonne indeformabili
-
punzone di ribattitura indeformabile
-
colonne di forma cilindrica e di sezione circolare (in realtà
hanno variazioni di sezione agli
estremi)
-
La trave ‘colonna’
soddisfa le ipotesi della teoria di De Saint Venant poiché
i carichi reali applicati sulla struttura sono forze di superficie
(sforzi = forza/area) distribuite agenti solo sulle basi (la sup. laterale è
scarica). Quindi per il principio di De Saint Venant è possibile considerare la
risultante di tali distribuzioni ed il momento risultante. Da indagini
analitiche si dimostra che tale
approssimazione implica un errore relativo ridotto
nelle zone sufficientemente lontane dalle basi (distanza > dimensione
massima della sezione) e un errore dipendente dalla reale distribuzione di
sforzi nelle zone prossime alle basi
-
materiale delle colonne acciaio C45 UNI EN 10204 –2.2-
(riferimento alle norme per il controllo di produzione). Prodotte per
deformazione plastica a freddo e allo stato di normalizzate con riporto
superficiale di cromo. Le caratteristiche meccaniche del C45 allo stato di
normalizzato sono: Rm= carico unitario di rottura = 610MPa ,
Rsn =
carico unitario snervamento = 350 MPa , A = allungamento percentuale =18% .
(tali caratteristiche meccaniche sono state riportate dal sito www.dalmina.it
il 26-02-‘04)
-
Le forze dovute all’attrito tra la testa del ribattino e la macchina sono
trascurabili rispetto alla componente normale
-
Durante la ribattitura la
forza verticale Fz è data dall’azione del pistone posto tra le colonne:
quindi non vi sono forze assiali che agiscono sulle colonne
- Le bullonature tra le colonne e le traverse non sono considerate ai fini dell’analisi della flessione. Ciò perché la flessione delle colonne è invariante sia che la traversa sia bullonata sulle colonne sia che siano un pezzo unico
- Il pistone di ribattitura spinge sulla traversa inferiore . Non vi è alcun vincolo tra traversa e pistone se non quello di tangenza per cui il pistone presenta solo azione assiale (ovviamente pari alla forza di ribattitura)
CASO FORZA ORIZZONTALE DIRETTA LUNGO ASSE Y: Fy
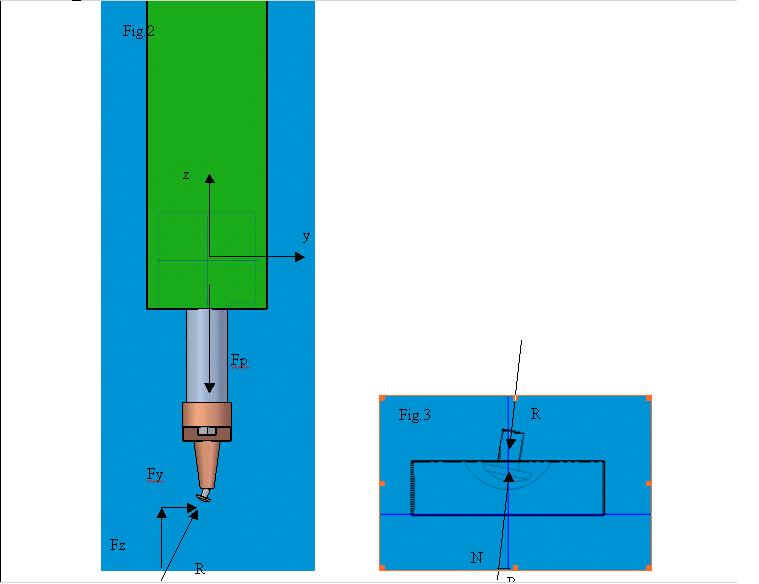
Analizziamo il caso in cui il ribattino si inclina di un
angolo B rispetto all’asse z nel piano yz.
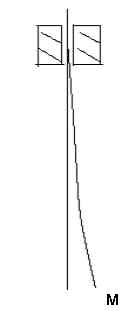
Nell’ipotesi che le forze di attrito tra il porta rivetto e la testa del medesimo siano trascurabili la reazione vincolare N è ortogonale alla superficie nel punto di contatto quindi è diretta come l’asse del rivetto stesso (si veda la figura 3).
Per l’equazione di equilibrio del rivetto: (prima
equazione cardinale della statica )
N = R
Dove R è la forza scambiata tra il rivetto ed il punzone
Essendo
N
= Fy j + Fz k
e B l’angolo direttore
Fy = ||N|| cosB
Fz = ||N|| sinB
Da cui
Fy = Fz.tg(B)
Tale formula ci permette di ricavare la componente orizzontale Fy data la forza di ribattitura del pistone Fp che per l’equilibrio alla traslazione verticale del sistema colonne-traversa è pari a Fz.
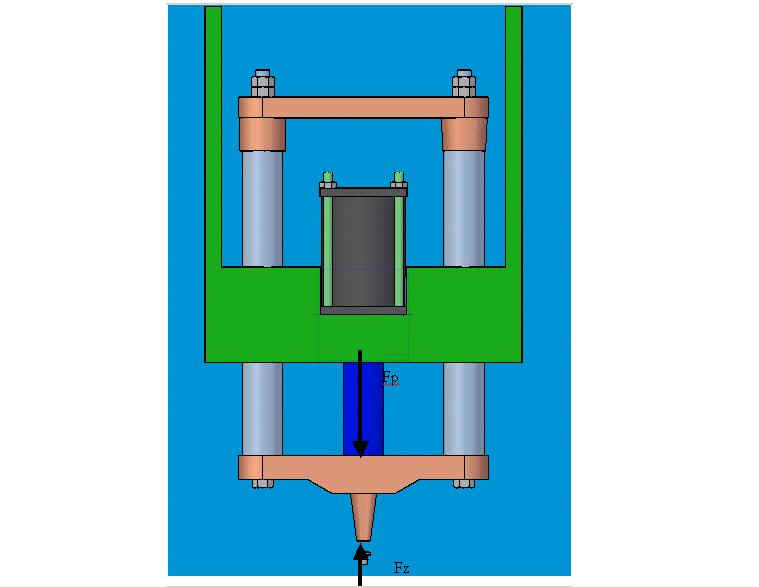
equazione equilibrio alla traslazione lungo asse z del
sistema colonne-traverse:
Fp = Fz .
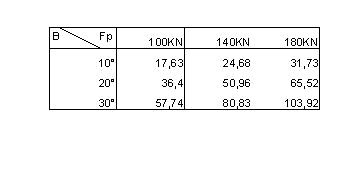
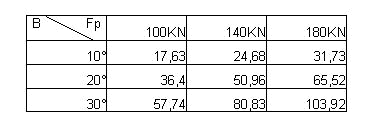
Dalle relazioni sopra dimostrate si ricava la seguente tabella a doppia entrata che riassume i 9 valori di forza Fy da considerare
CALCOLO DELLE REAZIONI VINCOLARI
Le boccole sono paragonabili a dei pattini quindi vincoli che nel piano eliminano 2 gradi di libertà introducendo due reazioni vincolari. Poiché tutte le forze esterne attive (forza del pistone, forza del rivetto R) sono sul piano zy anche le reazioni vincolari introdotte dalle guide giacciono su tale piano: una coppia Cx (il pedice x indica che il vettore è diretto lungo l’asse delle x) ed una forza ortogonale alla superficie di strisciamento Ry.
Nel piano zx le due boccole presenti introducono complessivamente 4 gradi di vincolo quindi la struttura è una volta iperstatica. Quindi per il calcolo delle reazioni vincolari è necessario ricorrere ad espedienti quali : simmetria della struttura, principio dei lavori virtuali, linea elastica.
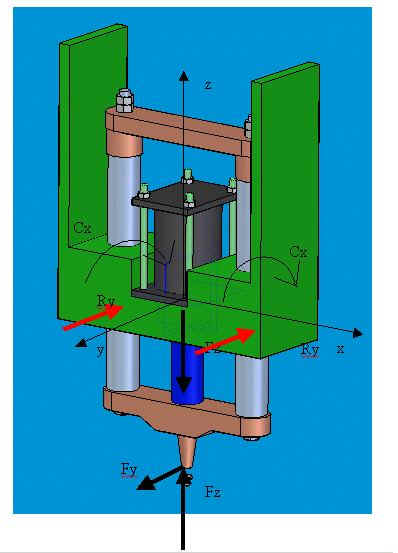
Per simmetria della struttura rispetto al piano zy è possibile concludere che anche le reazioni delle guide sono simmetriche. Infatti nella figura sono indicate con lo stesso nome.
Inoltre nell’ipotesi di asenza di gioco tra boccole e
colonne la reazione vincolare Ry è posta esattamente in corrispondenza
dell’inizio della boccola.
Seconda equazione cardinale della statica rispetto
all’asse x
SMx
= 0 (somma vettoriale dei
momenti rispetto all’asse x è
nulla)
2.Cx + 2.
Fy .
d = 0
Equilibrio alla traslazione lungo asse dell y:
2 .
Ry – Fy = 0
da cui
Ry = Fy/2
Cx
= - Fy .
d/2
Riportiamo i diagrammi di azione interna per la colonna
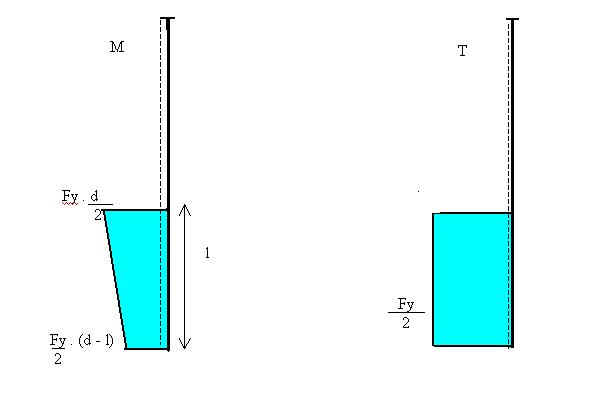
CALCOLO DELL' INFLESSIONE D
Abbiamo usato il teorema dei lavori virtuali sotto le seguenti ipotesi:
1. ipotesi di congruenza: le sezioni ruotano restando piane
2. piccole deformazioni
TEOREMA DEI LAVORI VIRTUALI PER CORPI DEFORMABILI
Enunciato:
‘ Una struttura deformabile è in equilibrio sotto l’azione di un sistema di forze se e solo se il lavoro virtuale delle froze interne è uguale al lavoro virtuale delle forze esterne per ogni deformata virtuale:
Lv
int =
Lv est
qualunque deformata virtuale
’
Considero due strutture una ‘reale’ ossia soggetta ai carichi reali dati dal problema ed una ‘di servizio ’ in cui si pone un carico fittizio unitario nel punto G di cui si vuole determinare la flessione.
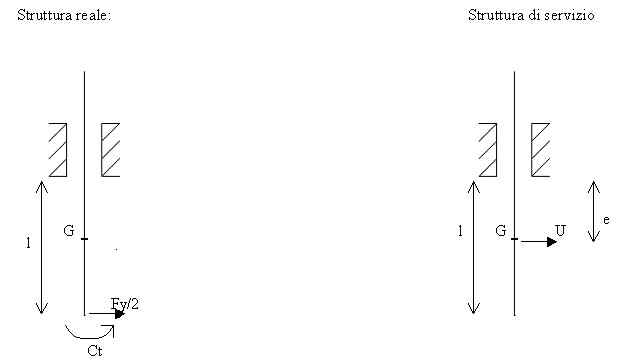
dove si indica con :
G = punto in cui si vuole determinare la flessione
Ct = momento di trasporto della forza Fy dalla punta dell’utensile all’estremità della colonna
Ct = (Fy/2)
. (d-l)
U = carico unitario applicato in G (= 1 N)
e = distanza del punto G dalle boccole
Dall'applicazione del teorema otteniamo i seguenti valori relativi all'inflessione della colonna
INFLESSIONE NEL PUNTO G (valori degli spostamenti espressi in mm)
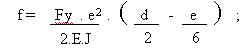
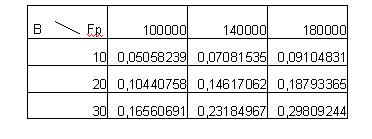
PUNTO DI MASSIMA INFLESSIONE
valori degli spostamenti espressi in mm
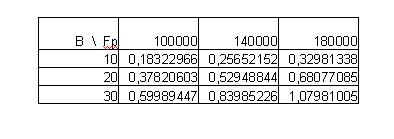
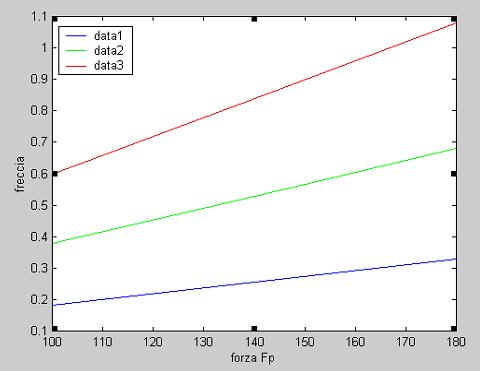
Grafico MATLAB relativo alla freccia (mm) in funzione dell'angolo B e della forza Fp.
data1 = spostamenti per B=10°
data2 = spostamenti per B=20°
data3 = spostamenti per B=30°
VERIFICA DI RESISTENZA STATICA DELLA COLONNA
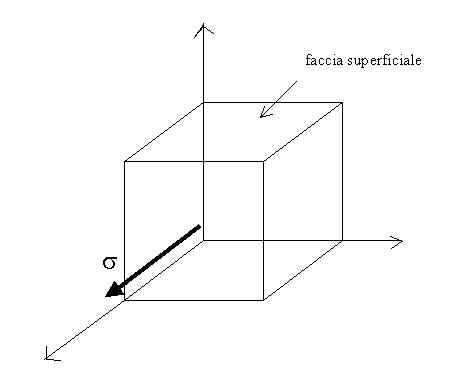
dove per una trave di sezione costante e longilinea vale la formula di De Saint-Venant:
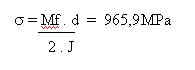
Il materiale della colonna è acciaio C45 quindi si tratta di un materiale duttile cioè che presenta un tratto di snervamento e di deformazione plastica. Pertanto è opportuno considerare un criterio di resistenza adatto per materiali duttili. Ad esempio si assume il criterio di Guest – Tresca
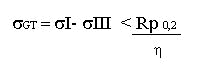
dove:
Rp 0,2 = carico unitario per il quale si ha una deformazione residua del materiale del 0.2%
Per il C45 bonificato: = 350 MPa
sigma I = sforzo principale massimo
sigma III= sforzo principale minimo
h
= coefficiente di sicurezza (min = 1.5 per materiali duttili)
Nel cubetto di
materiale considerato:
sigma I = sigma = 965,9 MPa
sIigma I = sigma III = 0
quindi si può affermare con certezza che
l’elementino della sezione in questione snerva sicuramente deformandosi
plasticamente:
sigma GT = 965,9 >> 350 (per Fmax=180 kN e B=30°)
Procedendo all’inverso è possibile determinare il valore di forza massimo a cui può essere usata la macchina in questione assumendo come sforzo limite lo snervamento e come coefficiente di sicurezza 1,5.
Per B=30°
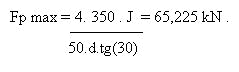
Vediamo la forza massma applicabile nel caso di differenti angoli:
Per B=20° : Fp max=68,97 kN
Per B=10° : Fp max=142,377 kN
FORZA ORIZZONTALE DIRETTA LUNGO ASSE X : FX
Procedendo analogamente al caso precedente si ottengono le tabelle relative alla situazione di forza orizzontale
tabella delle forze Fx (identica alla precedente ottenuta per il caso 1):
SCHEMA DELLA STRUTTURA E CALCOLO DELLE REAZIONI VINCOLARI
La struttura in questo caso è iperstatica (3 g.d.l., 4g.d.v.) per cui non posso a priori assumere Ca=Cb e Ra=Rb.Per l’analisi della flessione delle colonna si adotta il seguente schema
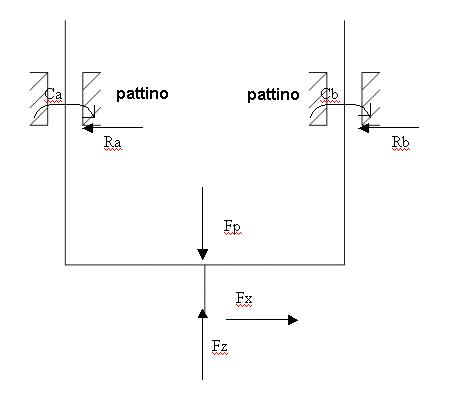
Le boccole sono paragonabili a dei pattini quindi vincoli che nel piano eliminano 2 gradi di libertà introducendo due reazioni vincolari. Poiché tutte le forze esterne attive (forza del pistone, forza del rivetto R) sono sul piano zx anche le reazioni vincolari introdotte dalle guide giacciono su tale piano: due coppie Ca e Cb e due forze ortogonali alla superficie di strisciamento Ra e Rb.
Nel piano zx le due boccole presenti introducono complessivamente 4 gradi di vincolo di cui due per la rotazione e due per la traslazione lungo x quindi la struttura è due volte iperstatica. Per il calcolo delle reazioni vincolari è necessario ricorrere ad espedienti quali : simmetria della struttura, principio dei lavori virtuali, linea elastica.
In questo caso non è giustificato assumere che le reazioni vincolari della struttura sono simmetriche in quanto è verificata la simmetria della struttura ma non la simmetria dei carichi. Quindi non è formalmente corretto assumere Ca=Cb e Ra=Rb, è opportuno dimostrarlo.
Pertanto per determinare le reazioni vincolari possiamo usare il principio dei lavori virtuali come metodo di calcolo delle forze vincolari. Si procede nel seguente ordine:
- si eliminano gli n gradi di vincolo iperstatici sostituendovi delle forze incognite Xi
- si considerano n strutture di servizio (una per ogni grado di vincolo eliminato) in cui si tolgono tutte le reazioni incognite tranne una al cui posto si pone un carico unitario
- si applica il principio dei lavori virtuali considerando come deformata la deformata reale in cui M = M(Xi) e gli spostamenti in corrispondenza del vincolo sono nulli
- così facendo per ogni reazione Xi incognita si ottengono n equazioni lineari a sistema nelle incognite Xi
Come prevedibile dalla simmetria della struttura, le reazioni vincolari delle due boccole sono uguali.
Ca = Cb = (Fx/2) d
Ra = Rb = (Fx/2)Per cui le azioni interne, le deformazioni, la verifica di resistenza sono uguali al caso precedente. Riportiamo le tabelle già viste nel caso precedente.
Inflessione nel punto G

Inflessione all'estremità inferiore della colonna

CASI IN CUI IL RIVETTO SI INCLINA IN UNA DIREZIONE QUALSIASI DEL PIANO XY
Per determinare di quanto flettono le colonne nel caso in cui il rivetto si inclini in una direzione qualsiasi occorre fare delle opportune considerazioni.
1) vi è una correlazione lineare tra la forza orizzontale
Fy e la deformazione delle colonne. Ciò è evidente dalla formula esplicita
ottenuta nel paragrafo 1.5.2 :
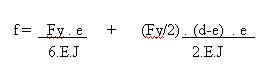
chiamando K la
costante di proporzionalità del legame :
f = K . F ;
2) una forza Fo definita su di un piano
può sempre essere scomposta in due componenti parallele a due assi
incidenti . In particolare la forza orizzontale causata dall’inclinazione del
rivetto può essere scomposta in due componenti Fox e Foy parallele
rispettivamente all’asse x ed
all’asse y :
|Fo| = Fp .
tg(B)
e
Fo = Fox i + Foy j ;
da cui per il teorema di Pitagora:
![]()
3) la sezione delle colonne è circolare pertanto il momento d’inerzia baricentrico J è uguale rispetto a qualsiasi asse passante per il centro. Quindi assegnata una forza di modulo fissato, al variare della direzione della forza nel piano xy la flessione della colonna è uguale in tutte le direzioni possibili.
Tradotto in termini matematici:
fx = K . Fx
fy = K . Fy
dove K , la costante di proporzionalità, è uguale sia per deformazioni lungo l’asse x che lungo l’asse y.
Ovviamente ciò non sarebbe vero se la sezione fosse
rettangolare. Avremmo dovuto considerare delle costanti di proporzionalità
Kx e Ky differenti a seconda della direzione della forza.
Dalle osservazioni 1), 2), 3) si deduce che è possibile
scomporre la forza Fo in due componenti Fox e Foy ognuna delle quali causa una
inflessione lungo il rispettivo asse di modulo direttamente proporzionale al
loro:
fx = inflessione lungo asse x = K .
Fox
fy = inflessione lungo asse y = K .
Foy
Quindi la risultante dell’ inflessione f è data dalla somma vettoriale delle due componenti ed ha modulo dato dal teorema di Pitagora:
![]()
da cui sostituendo:
f = K . Fo ;
Risultato:
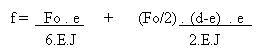
dove Fo = Fp .
tg(B)
ovviamente valgono le medesime tabelle per gli spostamenti ricavate sopra.
VERIFICA DI RESISTENZA STATICA DELLA COLONNA
Non riteniamo sia necessario riportala in quanto identica al caso precedente.
Lo scopo della relazione è stabilire la freccia massima della colonna in funzione della forza di ribattitura e dell’angolo di inclinazione del ribattino. Pertanto sono stati riportati i grafici Matlab in cui assegnato l’angolo B e la forza Fp è possibile ricavare la freccia o flessione della colonna sia nel punto X indicato che nell’estremità della colonna.Per completare la relazione abbiamo analizzato lo stato di sforzo del punto più sollecitato della colonna in funzione della forza Fp e dell’angolo B. Da tale analisi si nota che i valori di forza di pressione massima limite variano molto al variare dell’angolo critico B da 43 kN a 142 kN.Pertanto non è possibile fare una stima teorica accurata del carico massimo applicabile alla macchina.Per avere una stima molto accurata sarebbe opportuno misurare per quale inclinazione del ribattino B si ha la forza massima ad esempio fissando un trasduttore di spostamento LVDT sulla colonna : in questo modo è possibile determinare il valore dell’angolo in corrispondenza del quale si ha lo spostamento massimo.Oppure è possibile misurare direttamente la deformazione della colonna nella sezione più sollecitata applicando un estensimetro in prossimità della boccola. In questo modo tramite la legge di Hooke è possibile ricavare il valore dello sforzo normale. Tale procedura sarebbe molto pratica e economica dato il ridotto costo di un estensimetro rispetto ad un trasduttore LVDT.Inoltre è da considerare che tali valori sono stati ottenuti da un dimensionamento statico che non considera il fenomeno di fatica del materiale. Per operare una corretta verifica di resistenza a fatica illimitata sarebbe stato necessario conoscere esattamente il limite di fatica a flessione rotante del materiale, dato da noi non reperibile. Infatti o è necessario conoscere direttamente dal fornitore dell’azienda tale valore oppure avere un numero elevato di provini del materiale ed eseguirne la prova di flessione rotante. Si ottiene un sufficiente numero di dati per valutare il valor medio del limite di fatica.Pertanto è opportuno che prima di procedere alla progettazione della macchina l’azienda conosca i limiti di resistenza a fatica del materiale o lo ricavi da prove sperimentali oppure basandosi sui dati relativi al dimensionamento statico adotti coefficienti di sicurezza molto elevati (superiori a 3).Per applicazioni future sarebbe interessante eseguire la verifica di durata illimitata delle colonne a muovere dai dati fin qui riportati. Dati molto utili in quanto ottenuti risolvendo la struttura iperstatica e confermati dall’analisi ad elementi finiti che illustreremo di seguito.Il problema iniziale dell’analisi agli elementi finiti consiste nell’arrivare a conoscere lo stato di sollecitazione e di deformazione di un continuo deformabile a cui sono applicate delle trazioni sul contorno e sono presenti delle forze di volume e degli spostamenti imposti.
ANALISI AGLI ELEMENTI FINITI
Per studiare il problema è possibile utilizzare due approcci :
-Approccio agli spostamenti, che partendo dal campo di spostamenti ricava le deformazioni e lo stato di tensione, imponendo come unica condizione le equazioni indefinite di equilibrio che in questo caso sono le equazioni di Cauchy-Navier;
-Approccio allo stato di sforzo, in cui gli sforzi vengono assunti come incognite di partenza e oltre alle equazioni indefinite di equilibrio devono essere inoltre soddisfatte le equazioni di congruenza interna e va quindi impostato un sistema di equazioni differenziali con le opportune condizioni al contorno.
Il metodo agli elementi finiti utilizza il primo approccio e tiene perciò come incognita il campo di spostamenti da cui si ricavano tutti i risultati successivi.
Poiché le equazioni differenziali che devono essere risolte con le dovute condizioni al contorno sono tutt’altro che facilmente risolvibili per via analitica e necessaria una procedura numerica-approssimata utilizzando un calcolatore.
L’idea di base degli elementi finiti consiste nel suddividere il dominio del continuo in tanti sottodomini di dimensione inferiore ( come triangoli e quadrilateri nel caso piano e prismi e tetraedri nel caso tridimensionale ) nei quali è possibile utilizzare funzioni approssimanti più semplici proprio perché l’elemento è di dimensioni ridotte. Queste funzioni sono dette “funzioni di forma” o “shape functions” e per riportare i corretti valori nei nodi devono valere “1” nel nodo su cui è costruitia la funzione e “0” negli altri nodi.
Le shape functions possono essere di due tipi :
- Serendipity Elements : funzioni scelte con un metodo casuale che comunque rispettano i valori nei nodi e generalmente sono le più utilizzate ;
- Funzioni costruite a partire dai polinomi di Lagrange che però possono dare problemi di approssimazione dovute ad oscillazioni indesiderate.
Il campo degli spostamenti è calcolabile una volta che si conoscono gli spostamenti di certi punti particolari nell’elemento ( i nodi ) : questi spostamenti vengono chiamati spostamenti nodali.Il generico spostamento viene ricavato come sommatoria dell’i-esima funzione di forma per lo spostamento ( nelle direzioni degli assi principali ) dell’i-esimo nodo.
E’ quindi necessario riuscire a determinare il vettore degli spostamenti dei nodi. Definendo questo vettore con il simbolo íUý si dimostra che : [K]* íUý = í F ý.
[K] è la matrice di rigidezza ( o di “stiffness” ) e viene ricavata per integrazione numerica ( per esempio utilizzando il metodo di Gauss ). [K] è una matrice simmetrica e porta dentro di sé le informazioni riguardanti le caratteristiche del materiale e la geometria dell’elemento.
í F ý è il vettore delle forze nodali e viene ricavato anch’esso per integrazione utilizzando le funzioni di forma, i carichi esterni applicati (cioè il vettore delle trazioni ) e le forze di volume.
Per concludere vanno infine specificate le condizioni al contorno : per ogni grado di libertà dei nodi ( 2 gdl nel caso di analisi 2D, 3 gdl nel caso di analisi 3D ) è possibile specificare una forza o ( nel significato latino di “aut” ) uno spostamento.
Utilizzando le condizioni al contorno è inoltre possibile semplificare il problema se in presenza di eventuali simmetrie spezzando il problema a metà ed imponendo nei nodi uno spostamento nullo ortogonalmente al piano di simmetria ( asse x ) e una forza nulla ( che equivale ad uno spostamento libero) nel piano di simmetria ( lungo y e z ) in modo da velocizzare considerevolmente i tempi di calcolo.
Nel caso trattato successivamente con la forza simmetrica Fy non si è considerato comunque la divisione del pezzo lungo il piano yz poiché applicando lungo la parte spezzata dei vincoli di incastro ( “Fixed” ) verrebbero bloccati anche gli spostamenti lungo gli assi y e z e si verrebbe a creare un effetto di intaglio che provocherebbe delle zone di concentrazione degli sforzi falsando tutti i risultati ricercati. Probabilmente il software utilizzato è in grado di trattare problemi simmetrici ma né negli esempi proposti né nell’imposizione dei vicoli vi sono features che possano presagire a considerare eventuali simmetrie.In questo caso i tempi di calcolo computazionale non sono stati elevati e quindi il considerare il problema con il pezzo completo non ha causato problemi.
Per l’analisi agli elementi finiti si è utilizzato
il software “ Femap v8.1” in dotazione in forma ristretta per utilizzo
didattico nella nostra sede del Politecnico di Milano.
Per prima cosa è doveroso segnalare che Femap v8.1, almeno nella forma in dotazione in sede, non è in grado di implementare un’analisi per pezzi assemblati. Nel caso studiato è stato comunque sufficiente osservare come la parte di colonne che si deforma sia costituita principalmente dai 118 mm compresi tra la traversa inferiore e la cassa ed è quindi possibile semplificare il progetto disegnando un pezzo tagliato in Solid edge in monoblocco e salvandolo in formato STEP.
A questo punto è possibile lavorare in Femap
utilizzando i seguenti passaggi :
-IMPORTARE LA GEOMETRIA : partendo dal menu File si
seleziona la voce ImportàGeometry
e si sceglie il file.stp da importare. La scelta di un file.stp non è casuale
in quanto questo è un formato generale utilizzato per trattare i solidi nel
loro volume.
-INSERIRE I VINCOLI : dal menu Model si sceglie la voce “Constraint on Surface” à ciò equivale a dire che si vuole inserire dei vincoli su una superficie. Vengono quindi scelte le superfici da vincolare selezionando le basi superiori dei cilindri che costituiscono le due colonne guida e si individua il tipo di vincolo da applicare cioè l’incastro ( “Fixed” ).
Le colonne risultano quindi vincolate.
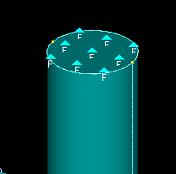
-APPLICARE I CARICHI: dal menu Model si sceglie la voce “Load on Surface” à ciò equivale a dire che si vuole inserire un carico su una superficie. Viene perciò scelta come superficie la base inferiore del punzone e “Force” come load inserendone il valore in Newton.
-DEFINIZIONE DEL MATERIALE: la lista dei materiali presente nella libreria del software è risultata francamente povera ( basti pensare che gli acciai presenti sono solo sette) , è comunque possibile impostare i dati manualmente. Ricordando che l’acciaio è del tipo C40 è, agli scopi dell’analisi, necessario inserire il modulo di elasticità di Young pari a 207000 MPa e la massa volumica dell’acciaio ( poiché è un campo obbligatorio richiesto dal programma ) che, in [ t / mm^3 ], è di 0,00000787. Il materiale inoltre è isotropo.
-STUDIARE I RISULTATI DELL’ANALISI
RIPORTIAMO I DISEGNI DEL SOLIDO ANALIZZATO
Fy (Spostamento)
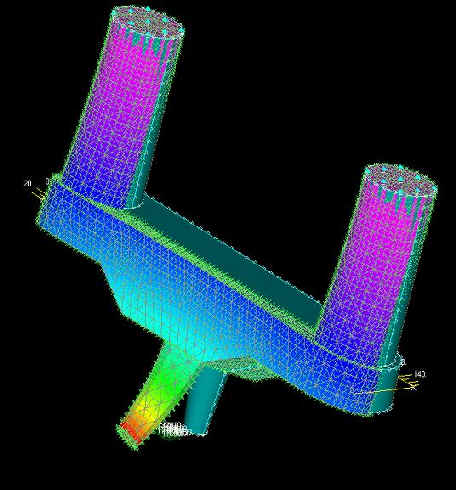
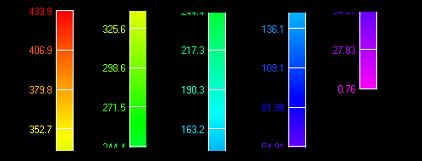
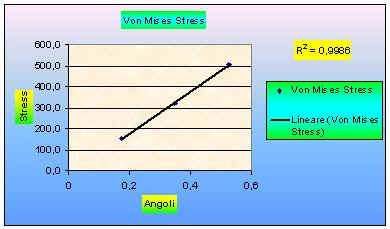
Fy (stress di Von Mises)
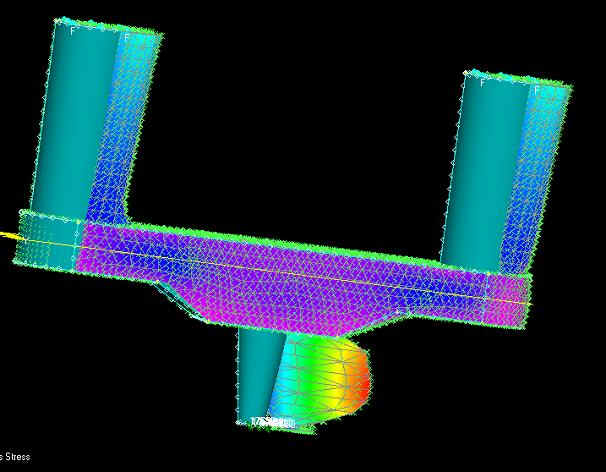

Fx (Spostamento)
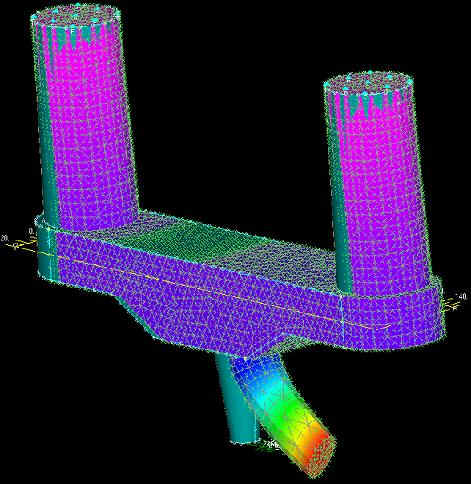
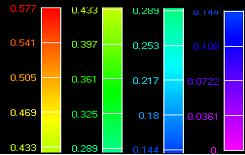
Fx (stress di Von Mises)

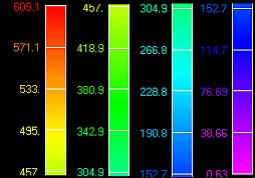
TRASLAZIONE VON MISES STRESS
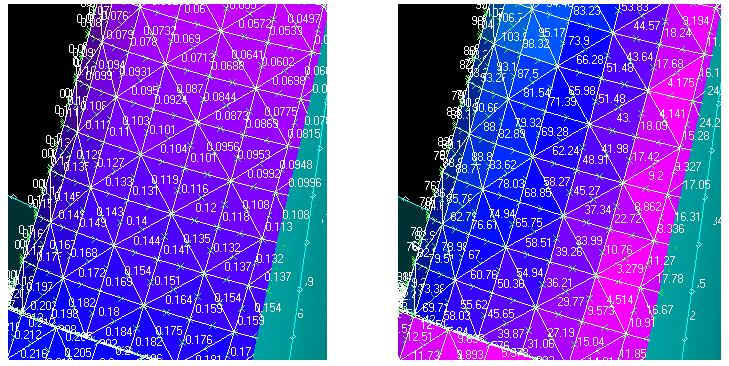
Analizzando le traslazioni e i diversi stati di sforzo ottenuti è stato possibile costruire delle tabelle dove sono riportati i dati ottenuti in Femap al variare del carico agente, della direzione del carico stesso e dell’inclinazione del ribattino.
Le forze sono espresse in kN, gli angoli sono
espressi in radianti, le traslazioni sono espresse in mm,
li
sforzi sono espressi in MPa .
Caso Fy (simmetrico)
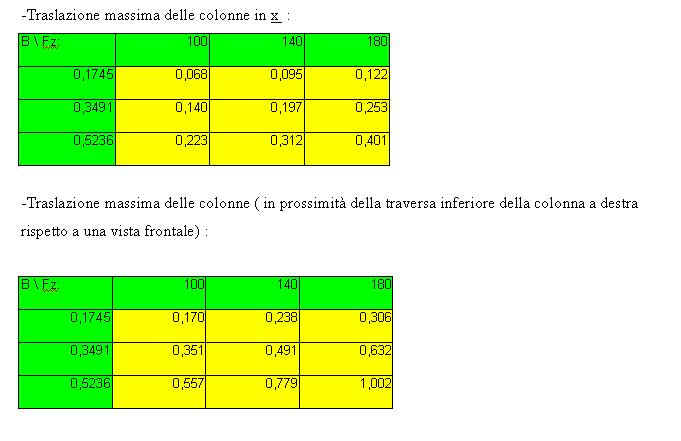
Traslazione massima delle colonne in X:
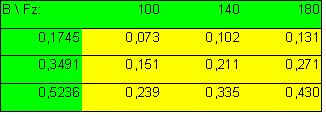
E’ possibile osservare come vi sia un andamento lineare della traslazione in x delle colonne al variare dell’angolo di inclinazione del ribattino ( sulle coordinate ) con una forza Fz costante di 100 kN e con conseguenti forze Fy variabili ( sulle ordinate )
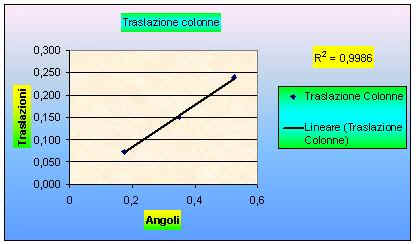
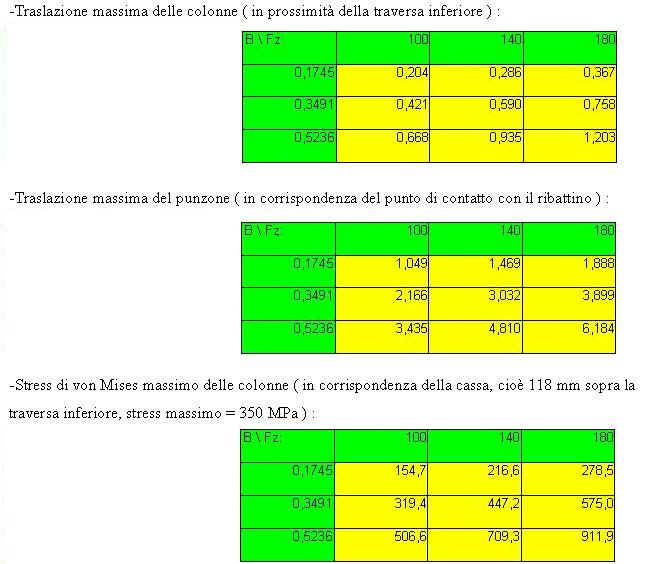
E’ possibile osservare come vi sia un andamento lineare anche dello stato di sforzo delle colonne al variare dell’angolo di inclinazione del ribattino ( sulle coordinate ) con una forza Fz costante di 100 kN e con forze Fy variabili ( sulle ordinate ).
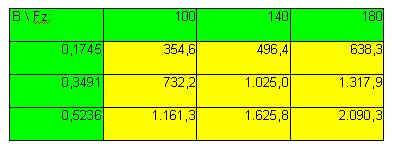
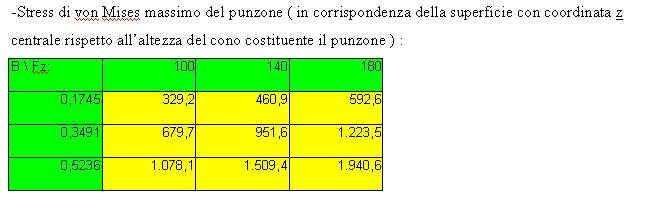
-Stress di von Mises massimo del punzone ( in corrispondenza della superficie con coordinata z centrale rispetto all’altezza del cono costituente il punzone ) :
Caso Fx (non simmetrico)
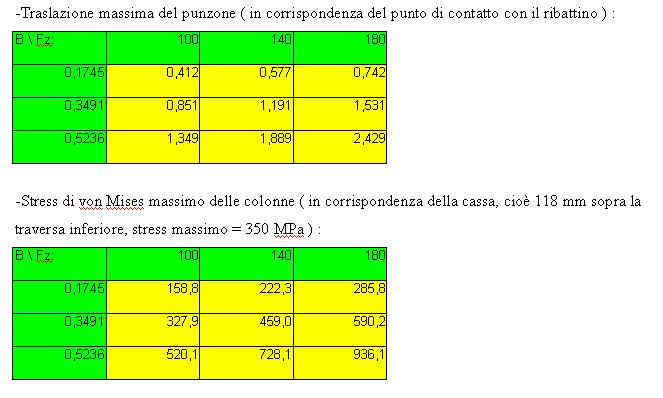
Per quanto concerne l'analisi agli elementi finiti è interessante riconoscere l'utilità di quest'ultima soprattutto per semplificare i conti su strutture non facilmente schematizzabili a livello manuale.Il problema principale è risultato essere il software che seppur potenzialmente molto ben articolato è purtroppo privo di un help adeguato in questa sede del Politecnico e nonostante le richieste via e-mail in riguardo presso l’azienda produttrice non si è riusciti a ricevere.Tuttavia al fine degli scopi proposti nel progetto l’utilizzo di Femap v8.1 è risultato essere del tutto soddisfacente grazie anche all’applicazione profusa nel cercare di apprenderne le funzionalità.
CONCLUSIONI E CONSIDERAZIONI FINALI
OSSERVAZIONI E CONFRONTI
Il progetto di analisi della flessione delle colonne di una rivettatrice è risultato essere per sua natura molto completo per quanto concerne lo studio ingegneristico del problema : infatti esso comprende un’analisi funzionale della struttura in esame, una modellazione parametrica dei componenti della struttura stessa, un’analisi tramite la scienza delle costruzioni ed un’analisi di tipo numerico computazionale agli elementi finiti.
Dopo una prima parte di studio del funzionamento della macchina per comprendere appieno tutti i vari aspetti e le problematiche inerenti la flessione delle colonne si è passati alla modellazione della struttura della rivettatrice : si è ritenuto opportuno utilizzare un modello di tipo parametrico al fine di rendere più agevoli futuri studi e di vincolare in maniera precisa e sicura le quote dei vari accoppiamenti. A tal fine è stata inclusa nel progetto anche una tabella Excel con i vari link associati alle variabili dimensionali dei pezzi per una gestione di essi visivamente e intuitivamente facilitata.
Si è quindi proceduto con la parte di costruzioni di macchine e di analisi degli elementi finiti :
volendo confrontare e commentare quindi in questa sede i risultati ottenuti rispettivamente dal calcolo analitico e da quello numerico è possibile indicare le seguenti considerazioni :
- I valori di stress e di deformazioni delle colonne calcolati sono sufficientemente coerenti tra loro: i valori ricavati dal metodo analitico e dal metodo numerico hanno un errore relativo massimo pari al 10,2% nel caso di forza diretta lungo l’asse y e spostamento massimo mentre del 7,2 % nel caso di forza diretta lungo l’asse x e spostamento massimo. Questi errori sono dovuti alle ipotesi semplificative dell’analisi analitica (traversa indeformabili e effetti degli sforzi di taglio sulla flessione trascurabili). Per i valori di sforzo si ha un errore massimo del 5,6% relativo al caso di forza lungo la direzione y e del 3,08% relativo al caso x.
- I valori di stress massimo sopportabili dalle colonne risultano essere molto variabili a seconda dell’angolo di inclinazione del rivetto. A tal proposito nel capitolo di Costruzioni di macchine si sono trovate tre diverse situazioni di carico massimo sopportabile dalle colonne : questi carichi sono inferiori a quelli forniti dall’azienda Capmac, non a caso essa ci ha in seguito informati spiegando che i valori di forza forniti per calcolare la flessione sulle colonne erano indicativi e, anzi, servivano appunto per verificare quale fosse il carico massimo sopportabile. In questa situazione sono di conseguenza estremamente utili le tabelle riportate nel capitolo dell’analisi degli elementi finiti dove sono evidenziate tutti gli stress e le deformazioni per ogni caso studiato e si può facilmente osservare quando vengono superati i valori massimi ;
- Per quanto concerne il valori ricavati per il punzone sono stati calcolati dei risultati considerevoli : tuttavia esso costituito da una sezione variabile e le sue dimensioni da disegno sono risultate essere francamente troppo ridotte; appunto per questo si è ritenuto opportuno inserire i valori dei diametri delle basi superiore ed inferiore del punzone nella parametrizzazione del modello nonostante l’analisi del punzone non occupi un ruolo di primo piano nello studio della flessione delle colonne.
Nel progetto sono quindi inoltre inseriti due file Excel uno contenente le tabelle e i grafici degli stati di sforzo e di deformazione ricavati e l’altro costituito dalla tabella riguardante la variabili indipendenti parametrizzate del modello tridimensionale.
E’ infine presente una presentazione dell’azienda che produce la rivettatrice studiata.
RINGRAZIAMENTI
Si ringraziano i docenti del corso di “Laboratorio Progettuale assistito da calcolatore” per l’aiuto riguardante lo sviluppo del progetto ( e per l’averci accompagnato a Rho a visitare l’azienda ) e la “ Capmac s.r.l ” e il sig. Nicola Capelli per aver dato la possibilità di visionare in prima persona la sede e per le puntuali risposte agli e-mail inviati.
La
società Capmac s.r.l. è un’azienda che opera nel campo delle rivettatrici
speciali che, grazie a cospicui investimenti negli ultimi anni ha sviluppato
tecnologie innovative di rivettatura, sia autoforanti che per parti preforate,
per il settore del pentolame e per altre applicazioni. Ha inoltre realizzato
impianti multi-ribattino completamente automatizzati anche di grandi dimensioni.
La
Capmac lavora oggi con oltre 300 clienti, l’80% dei quali sono ubicati
all’estero, ed è leader mondiale nella produzione di rivettatrici, anche
speciali.
La
Capmac è membro attivo di Global Choice, un’unione di aziende italiane che
tramite la cooperazione sono in grado di soddisfare maggiormente gli interessi
loro e del cliente.
Info:
www.capmac.it