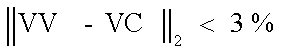1) Disegno tridimensionale delle varie dimensioni di tamburi:
Il tamburo è la parte della betoniera che ha il compito di contenere e di mescolare il calcestruzzo ed ha la caratteristica di essere assialsimmetrica e a simmetria cilindrica e tronco-conica. Viste le sue caratteristiche si è deciso di modellarla attraverso una protrusione di rivoluzione. I passaggi seguiti sono stati:
- Apertura di un documento part vuoto e disegno del profilo del tamburo da 12 m3
In seguito abbiamo usato il comando di protrusione di rivoluzione dove è stato scelto l’asse tratteggiato come asse di rivoluzione.
- Una volta creato il solido di rivoluzione “pieno” abbiamo impostato
attraverso il comando “thin wall” ![]() uno
spessore di 5 mm, e la faccia circolare a destra come zona di apertura.
uno
spessore di 5 mm, e la faccia circolare a destra come zona di apertura.
Il risultato è quello seguente:
Ora abbiamo bisogno dei modelli da 10 e 12 m3 ma questa volta, invece di ridisegnare i tamburi, ci avvaliamo della parametrizzazione. Poiché i tre tamburi differiscono tra loro solo per la larghezza della fascia cilindrica centrale basta rendere la quota di questa parametrizzabile. Con questo espediente riusciamo a ottenere i tamburi da 8 10 e 12 m3 solo variando la quota in 500 mm, 1000 mm e 1550 mm rispettivamente.
2) Espediente per simulare il riempimento:
La seconda parte del progetto consiste nel ricavare le coordinate del baricentro del calcestruzzo al variare dell’altezza del riempimento, quindi dobbiamo costruire un “solido” che sia tangente in ogni punto al tamburo e che abbia una faccia sempre orizzontale. Dai dati fornitici dall’azienda sappiamo che il tamburo è montato sullo chassis con una inclinazione del suo asse di 13°.
Per modellare il riempimento abbiamo agito in questo modo:
- Abbiamo creato un documento assembly in cui abbiamo importato il nostro tamburo.
- Nel documento assembly abbiamo creato un nuovo part utilizzando l’approccio bottom-up e cioè modellandolo con l’ausilio di una superficie fittizia coincidente con la superficie interna del tamburo.
- Con il comando “includi” abbiamo creato il profilo del solido di rivoluzione “riempimento” (coincidente con il profilo della superficie fittizia). Dopo aver disegnato il solido interno abbiamo ottenuto la seguente situazione.
(la superficie rosa e grigia indica la tangenza tra la superficie esterna del solido e la superficie fittizia)
- Abbiamo costruito un sistema di riferimento atto a ricreare l’inclinazione di 13° e per fare ciò abbiamo ruotato il piano orizzontale di 13° in senso orario e successivamente abbiamo inserito un piano parallelo a quest’ultimo e tangente alla sezione tronco-conica situata nella parte sinistra del tamburo.
- infine abbiamo utilizzato la funzione cutout di protrusione su un piano parallelo al piano precedentemente costruito. Infine abbiamo soltanto imposto di tagliare tutto ciò che è al di sopra del nostro piano e abbiamo ottenuto ciò che volevamo.
- Salvato il part in questione e riaperto il file assembly otteniamo il seguente risultato:
3) Acquisizione coordinate baricentro per ogni modello di tamburo.
Successivamente il nostro compito si è incentrato nel trovare un metodo di calcolo del baricentro del riempimento di calcestruzzo al variare della quota H. Per fare ciò abbiamo utilizzato una funzione presente in Solid Edge che è in grado di calcolare il baricentro di un qualsiasi corpo, quindi abbiamo semplicemente scelto un intervallo di discretizzazione e per ogni valore abbiamo trascritto le coordinate in una tabella.
Il sistema di riferimento è tale per cui l’origine degli assi coincida con il centro dell’apertura circolare del tamburo, il piano individuato dagli assi z e x sia tangente all’apertura stessa e z sia verticale.
Nel materiale consegnatoci si fa riferimento ad una altezza massima di riempimento, ma poiché non ci è stato possibile contattare il responsabile per ottenere maggiori informazione in merito, abbiamo deciso di calcolare il baricentro fino ad una altezza tale per cui il volume calcolato fosse pari al volume nominale del tamburo. Di conseguenza il tamburo da 8 m3 ha una altezza massima pari a circa 1550 mm, quello da 10 m3 ha una altezza di 1700 mm e infine quello da 12 m3 di 1800 mm. È importante sottolineare che tutte le coordinate risultano essere negative ad eccezione della x che rimane sempre pari a 0 (il che è intuitivo visto che il riempimento è simmetrico al piano zy).
4) Formulazione di leggi atte a stabilire la variazione della posizione del baricentro in funzione del riempimento del calcestruzzo
Una volta stilata la tabella con i valori necessari ci avvaliamo del ausilio del programma Excel con il quale riusciamo a ricostruire i grafici dell’andamento delle coordinate in funzione dell’altezza H di riempimento. Una volta pronti i grafici abbiamo calcolato il polinomio che interpola i dati trovati, così facendo abbiamo trovato una equazione che approssima l’andamento del baricentro. Per l’andamento della coordinata z è stata scelta una interpolazione di primo grado mentre per la coordinata y una di secondo grado. Gli errori tra il valore calcolato da Solid Edge, che abbiamo assunto come “valore vero”, e il valore calcolato sono molto piccoli: