|
Considerate due ruote dentate in presa si ha che:
ω1 velocità angolare di rotazione del pignone ω2 velocità angolare di rotazione della ruota condotta n1 numero di denti della prima ruota n2 numero di denti della seconda ruota
modulo: m = d/n Per due ruote dentate in presa, si ha che m1=m2
rapporto di trasmissione: i = ω1/ω2 rapporto di ingranaggio: u = n2/n1
i ~ u, ovvero ω1/ω2 = n2/n1 Definita P la potenza erogata dal motore, P = C*ω1 = C*ω2 Attraverso il valore della coppia e dell’angolo di pressione α (20°), possiamo definire il valore delle forze T tangente e R radiale, per ottenere poi il valore della risultante S, utilizzata nell’analisi fem.
C = T*d/2 R = T*tgα
Detta v la velocità di traslazione orizzontale e d il diametro della ruota:
v = ω*d/2 ovvero ω =2*v/d P = C*ω ovvero C = P/ω
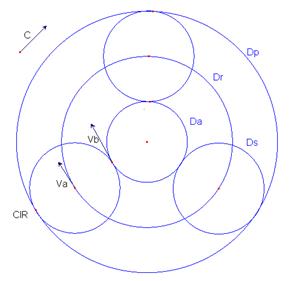
Consideriamo ora l’intero meccanismo, ovvero la ruota dentata dell’albero, le tre ruote dei satelliti e il porta satelliti. Di queste ruote rendiamo come riferimento per i nostri calcoli le circonferenze primitive. Si avrà quindi:
Diametro primitiva porta satelliti: Dp Diametro primitiva satelliti: Ds Diametro primitiva albero: Da Circonferenza di rotazione degli assi dei satelliti: Dr
Va = ω*Dr/2 Vb = 2*Va ωalbero = 2*Vb/Da C = P/ωalbero
Ora che siamo riusciti a calcolare il valore della coppia, possiamo calcolare le forze totali in gioco tra i denti a contatto: Tt = 2*C/Da Rt = T*tgα St = T/cosα
Essendo i satelliti tre ruote identiche e equidistanti, è intuitivo pensare alla risultante delle forze S come: S = St/3
Allo stesso modo possiamo ragionare per la potenza, che sarà equiripartita: Ps = P/3 Ws = 2*Va/ Ds C = Ps/ ω
Dall’equilibrio alla rotazione nel centro della ruota condotta si avrà:
Sa*r - Ss*r = -C Ss = Sa+C/r
|
|
CINEMATISMO |