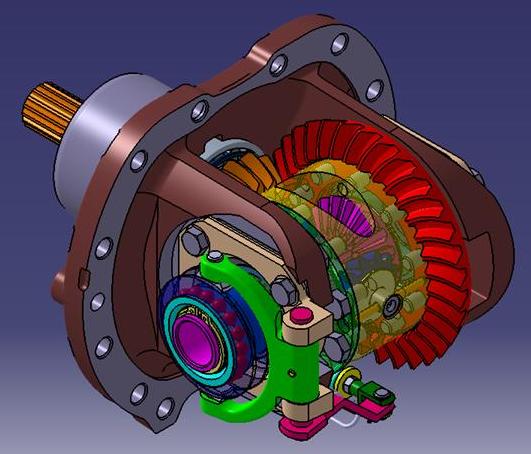
Il Differenziale

In un veicolo a motore, qualunque sia il numero delle ruote, vi sono uno o più assi preposti alla funzione di movimentazione del veicolo, le ruote montate su questo asse quindi non sono solo portanti ma anche motrici.

E’ facile immaginare come le ruote di un assale motore non possano essere indipendenti (tranne qualche caso di sistema di trazione sofisticato utilizzato su veicoli speciali, dove su ogni ruota viene montato un motore idraulico). Non possono però neppure essere vincolate rigidamente ad un albero in quanto in curva le ruote interne, quelle verso il centro di curvatura, descrivono un cerchio di raggio minore rispetto alle ruote esterne che sono più lontane dal centro; in altre parole le ruote interne e le ruote esterne percorrono tratti di strada diversi. Da qui la necessità di adottare un dispositivo capace di collegare le ruote interne ed esterne, in grado però di differenziare il numero di giri delle stesse al momento di affrontare una curva. Il dispositivo meccanico in grado di assolvere a tale funzione, prende giustamente il nome di Differenziale.

Il Differenziale fu applicato all’automobile nel 1898 da Péqueur, ma era già conosciuto in precedenza.

Praticamente il Differenziale è costituito dalla scatola, che riceve il moto da una ruota dentata, cilindrica o conica in funzione del layout del veicolo, uno o più perni portasatelliti (in funzione delle forze in gioco) solidale/i con la scatola, sul/i quale/i sono liberi di ruotare appunto i satelliti che sono ruote dentate coniche, che a loro volta ingranano con due ruote dentate coniche a 90° più grandi dette planetari, sui quali viene calettato il semiasse che porta il moto alle ruote. Il differenziale da noi trattato presenta una sola coppia di satelliti e di conseguenza un solo perno portasatelliti.

Il moto viene quindi trasmesso alla scatola dalla ruota dentata ad essa solidale, che a sua volta trasmette il moto al perno portasatelliti il quale forza i satelliti a compiere dei giri di rivoluzione; i satelliti, in presa con i planetari, fanno compiere agli stessi il movimento di rotazione attorno al proprio asse che andrà alle ruote.

Come abbiamo visto tutti gli elementi della catena cinematica sono sempre collegati; ora si deve analizzare la peculiarità del differenziale che, come detto sopra, ha la capacità di collegare costantemente le ruote, ma è in grado di differenziare i giri delle stesse.

Supponiamo di procedere lungo una traiettoria rettilinea dove le ruote di destra e di sinistra incontrano la stessa resistenza all’avanzamento: la coppia resistente che arriva dalle ruote ai due planetari sarà la stessa quindi le forze che si scambiano i denti del planetario destro e del planetario sinistro con i denti dei satelliti saranno uguali. In queste condizioni, il momento risultante rispetto all’asse del perno è nullo e quindi i satelliti non ruotano attorno al proprio asse. La velocità relativa tra le dentature dei componenti (planetari e satelliti) è nulla e quindi la ruota sinistra e la ruota destra compiono un ugual numero di giri che sarà lo stesso dei giri in input della scatola.

Quando si affronta una curva invece la ruota esterna offre meno resistenza all’avanzamento, la coppia resistente sul planetario sarà inferiore e quindi la forza che si scambiano i denti del planetario collegato alla ruota esterna con i satelliti sarà inferiore alla forza scambiata tra i denti del planetario della ruota interna e i satelliti. Venendo meno l’equilibrio prima discusso i satelliti saranno indotti a ruotare attorno al proprio asse. In questo caso, al contrario di prima, tra le ruote dentate coniche del Differenziale c’è velocità relativa; i satelliti compiono un moto di rivoluzione ma anche di rotazione attorno al proprio asse e quindi il differenziale si comporta come un rotismo epicicloidale.

Praticamente in curva il differenziale è in grado di far compiere un numero di giri diverso alle ruote esterne e interne, mantenendone però il collegamento e quindi la trazione.

Un legame cinematico tra le velocità di rotazione dei due planetari e la velocità di rotazione della scatola, si può ricavare dalla formula di Willis che esprime il rapporto di trasmissione del rotismo epicicloidale:

(1)

dove T= rapporto di trasmissione, n= numero di giri/min del portatreno (scatola), n₁= numero di giri/min del planetario sinistro, n₂= numero di giri/min del planetario destro; praticamente il rapporto di trasmissione risulta essere il rapporto tra le velocità relative dei due planetari rispetto al portatreno.

Se si considera il rotismo come ordinario, mantenendo fermo il portatreno (n = 0) e considerando uno dei due planetari motore e l’altro condotto si perviene al seguente risultato:

(2)

T risulta essere uguale a ‘–1’ poiché i due planetari ruotano ovviamente alla stessa velocità ma in senso opposto.

Nel caso in cui l’organo motore sia invece il portatreno, come effettivamente succede, e tenendo presente che il rapporto di trasmissione fra i due planetari è pari a ‘-1’, si può ricavare n il numero di giri del portatreno, in funzione dei numeri di giri dei due planetari n₁ e n₂:

(3)

Si presentano, come già discusso, due casi:

: si sta procedendo lungo una traiettoria rettilinea ed il rotismo risulta essere ordinario

: si sta affrontando una curva con resistenze alle due ruote diverse e nasce l’esigenza di differenziare il numero di giri delle due ruote secondo la (3); in questo caso il rotismo diventa epicicloidale. Sempre sfruttando la (3) si è in grado di spiegare perché nel momento in cui una ruota perde totalmente aderenza ruoti con una velocità doppia rispetto alla scatola. In questa situazione infatti l’altra ruota necessariamente si ferma; ponendo per esempio n₂ = 0 nella (3) si ottiene:

(4)

Questa condizione limite è da evitare perché porterebbe all’arresto del veicolo.