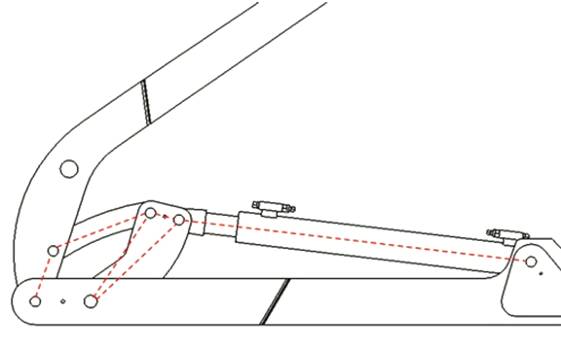
LA CINEMATICA

Dopo la fase di modellazione e assemblaggio  è particolarmente interessante  studiare il meccanismo dal punto di vista dinamico mettendo in evidenzia le forze che i vari componenti si scambiano tra di loro. Tuttavia ci scontriamo in primo luogo con l’esigenza di conoscere la cinematica del problema in particolare di ricavare lunghezze ed angoli.
Il braccio meccanico si comporta come un meccanismo piano; in particolare rappresenta l’unione di un quadrilatero articolato con un attuatore meccanico. La figura e il filmato seguente mostrano con più chiarezza la struttura e il funzionamento del cinematismo studiato.

ANIMAZIONE

Al fine di eseguire i calcoli, il cinematismo può essere così rappresentato :

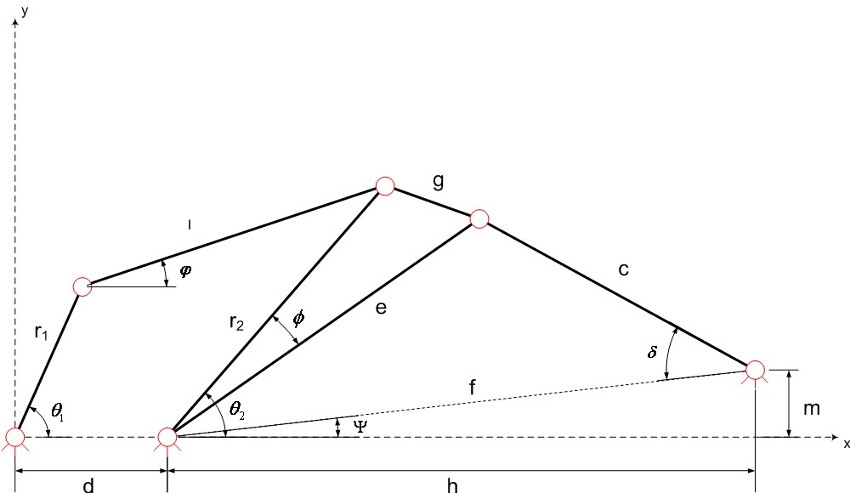
Innanzitutto focalizziamo l’attenzione sul quadrilatero articolato. La prima considerazione riguarda i valori delle lunghezze, in particolare le quattro lunghezze ci danno indicazione sulla mobilità dell’asta in ingresso e di uscita in base alla regola di Grashof. Indicando con M l’asta più lunga, con m quella più corta, e con r e s le restanti lunghezze, la regola di Grashof si può sintetizzare nella seguente forma:

Nel nostro caso si hanno le seguenti lunghezze:

Siccome il numero di Grashof è positivo, il quadrilatero articolato viene definito  a doppio bilanciere. Questo sta a significare che l’asta in ingresso e quella di uscita non sono in grado di eseguire una rivoluzione completa durante il moto del sistema ma sono limitate ad oscillare tra due posizioni angolari estreme.

 La determinazione per via analitica del rapporto di trasmissione, e, più in generale delle leggi di spostamento, velocità e accelerazione, richiede di pervenire ad una espressione che permetta di ottenere i valori di tali grandezze.
Il modo più rapido è il seguente: ricavare i legami geometrici ottenendo la legge degli spostamenti da cui, per derivazioni successive, dedurre le velocità e accelerazioni. Quindi si può scrivere la seguente relazione:

con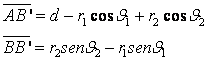             

Sostituendo si ottiene un’espressione che non è semplice da risolvere. Tale inconveniente può essere risolto impostando il calcolo in modo differente.

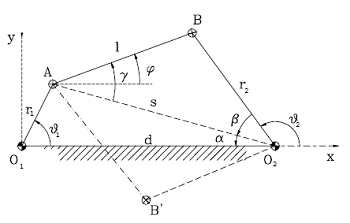
Definiamo la lunghezza della diagonale come

Sfruttando il teorema di Carnot si ottiene:

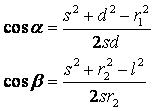
I valori degli angoli α e β consentono di avere il valore dell’angolo del braccio di uscita nella forma:

Sfruttando ancora il teorema di Carnot, si ricava

A differenza degli altri metodi, abbiamo ottenuto un calcolo semplice e sequenziale , cioè utilizzabile in procedimenti di calcolo automatico. È possibile per derivazione ottenere anche l’espressioni della velocità e accelerazione angolare ma nel nostro caso l'interesse verte più che altro sugli spostamenti prodotti dal cinematismo dutante il suo moto

Ora possiamo passare ai calcoli cinematici della parte restante del cinematismo.

Attraverso relazioni trigonometriche si ricava

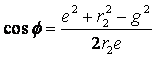                                    da cui si ottiene    13,126 °

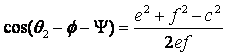
                        con        5,234°

Trovato il  valore di c, a questo punto è possibile ricavare il valore dell’angolo delta

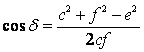
Riportiamo tutti i risultati ottenuti: