Contact Pressure Analysis
Contact pressure is calculated on the surface contact between cam and hook in order to evaluate contact pressure and strain between the two components. This is possible with the Hertzian theory of non-adhesive contact.The following assumptions are made in determining the solutions of Hertzian contact problems:
• the strain are small and within elastic limit
• each body can be considered an elastic half space
• the surfaces are continuos and non conforming
• the bodies are in frictionless contact
Driving force in extraction and insertion of the hook were calculated through dynamic simulation.
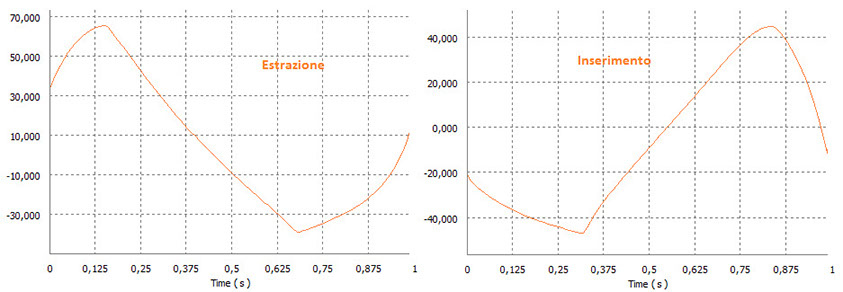
(Driving Force in estraction and insertion)
The force normal to the surface, necessary for the Hertzian therory, can be calculated with the following formula:
where:
• Fdrive is the driving force applied to the hook
• alpha is the angle between the two forces
• F is the force normal to the surface
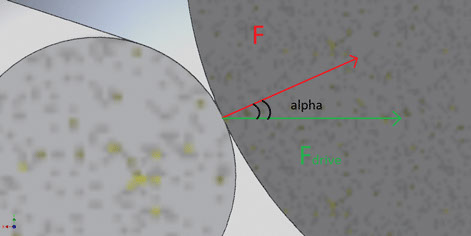
Via mathematical consideration we can demonstrate that the norm of F is maximum when the alpha angle is zero.
The contact surface of the hook is cilindrical, while the cam has a complex geometry. For this reason the cam has been simplified with cilindrical surface with different radius in the different situations studied.
The formulas from the Hertz theory utilized are:
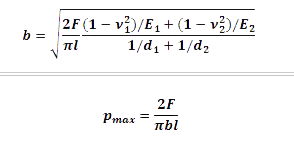
where:
• 'b' is half the lenght of the rectangular contact area
• 'pmax' maximum Hertzian pressure on the contact surface
• 'l' is the width of the contact area, equal to 5 mm
• 'E' is the elastic module of the material from the case and the hook, in particular Ecamma=7.8 Gpa e Ecase=9 Gpa
• 'F' is the force normal to the contact area
• 'd' are the diameters of the two components in contact
• 'nu' is the poisson coefficient of the two components, both equals to 0,4
Extraction:
• Fdrive = 33.7 N
• alpha ~ = 30 deg
• F ~= 29.18 N
• d_perno = 4.3 mm
• d_camma = +∞
Values found:
• 2b = 0.082 mm
• Pmax = 67.1 Mpa
• profondità superficie di contatto = 0.032 mm
Insertion:
• Fdrive = 22.27 N
• alpha ~ = 45 deg
• Fnorm ~=16.051 N
• d_perno = 4.3 mm
• d_camma = 13 mm
Values found:
• 2b = 0.052 mm
• Pmax = 61.9 Mpa
• profondità superficie di contatto = 0.021 mm
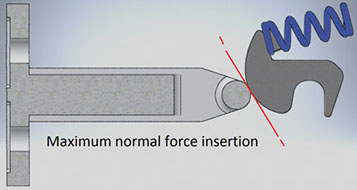
In conclusion from analisys of the contact pressure we can see that in both cases le stress on the contact area is under the yield strenght and the strain is inside the range of acetable values for a drier doorlock.
Source:
Laboratorio Progettuale CAD - Academic year 2015-2016

