

|
politecnico di milano |




|
Laboratorio progettuale CAD - A.A. 2010/2011
|
|
Script di Matlab in dettaglio |
|
clc clear all close all tic %avvio conteggio durata script ah=10.85; %lunghezza vettore fisso fi=pi/2+15/180*pi; %angolo vettore fisso alfa=15/180*pi; k=pi-2*alfa; %sfasamento fra alfa e alfaprimo AB=[]; %inizializzazione vettori BD=[]; DE=[]; EH=[]; AC=[]; FE=[]; CF=[]; DK=[]; ANGOLI=[]; i=1;z=1; %flag da utilizzare nella barra di progresso %dati per il calcolo delle forze FORZE=[]; Cmolla=15; %coppia mollone Fcont=0.3*9.81; %forza dei contatti bcont=22; %braccio fra contatto e centro del disco
%inizio dei cicli delle lunghezze, per ogni ciclo viene %dato un certo range in cui spaziare e un passo di variazione %lunghezze in mm
for ab=[3:2:7] barra=waitbar(i/3,'Attendere...'); i=i+1; for bd=[6:3:15] for de=[6:2:12] for eh=[6:2:12] for ac=[3:2:7] for fe=[6:2:12] for cf=[6:3:15] if ab+bd+de+eh>ah && ac+cf+fe+eh>ah F=@(x) [-ah*cos(fi)+ab*cos(alfa+k)+bd*cos(x(1))+de*cos(x(2))+eh*cos(x(3)); -ah*sin(fi)+ab*sin(alfa+k)+bd*sin(x(1))+de*sin(x(2))+eh*sin(x(3)); -ah*cos(fi)+ac*cos(alfa)+cf*cos(x(4))+fe*cos(pi+x(2))+eh*cos(x(3)); -ah*sin(fi)+ac*sin(alfa)+cf*sin(x(4))+fe*sin(pi+x(2))+eh*sin(x(3))]; [angoli,fval,exitflag]=fsolve(F,[pi/2 pi/2 pi/2 pi/2],optimset('Display','off')); %si è aggiunta nelle opzioni della fsolve la stringa per impedire che %stampi a schermo a ogni ciclo messaggi della funzione
if exitflag==1 dk=de+fe+8; b=[-Cmolla-Fcont*bcont 0 0 0]'; %termini noti nel sistema della forze if angoli(1)>=pi/2 && angoli(1)<=pi && angoli(4)>=0 && angoli(4)<=pi/2 %config 1 A=[ 0 abs((cos(angoli(1))*ab*sin(alfa+k))-abs(sin(angoli(1))*ab*cos(alfa+k))), abs((sin(angoli(4))*ac*cos(alfa))-abs(cos(angoli(4))*ac*sin(alfa))) 0; +cos(angoli(3)+pi) +cos(angoli(1)+pi) +cos(angoli(4)+pi) 0 ; +sin(angoli(3)+pi) +sin(angoli(1)+pi) +sin(angoli(4)+pi) 1 ; (cos(angoli(3)+pi)*de*sin(angoli(2))+sin(angoli(3)+pi)*de*cos(angoli(2))), 0 (cos(angoli(4)+pi)*(de+fe)*sin(angoli(2))+sin(angoli(4)+pi)*(de+fe)*cos(angoli(2))), dk*cos( angoli(2))];
else if angoli(1)>=0 && angoli(1)<pi/2 && angoli(4)>0 && angoli(4)<pi/2 %config 2 A=[ 0 -abs((cos(angoli(1))*ab*sin(alfa+k))-abs(sin(angoli(1))*ab*cos(alfa+k))), abs((sin(angoli(4))*ac*cos(alfa))-abs(cos(angoli(4))*ac*sin(alfa))) 0; +cos(angoli(3)+pi) +cos(angoli(1)+pi) +cos(angoli(4)+pi) 0 ; +sin(angoli(3)+pi) +sin(angoli(1)+pi) +sin(angoli(4)+pi) 1 ; (cos(angoli(3)+pi)*de*sin(angoli(2))+sin(angoli(3)+pi)*de*cos(angoli(2))), 0 (cos(angoli(4)+pi)*(de+fe)*sin(angoli(2))+sin(angoli(4)+pi)*(de+fe)*cos(angoli(2))), dk*cos(angoli(2))];
else if angoli(1)>0 && angoli(1)<pi/2 && angoli(4)>pi/2 && angoli(4)<=pi %config 3 A=[ 0 -abs((cos(angoli(1))*ab*sin(alfa+k))-abs(sin(angoli(1))*ab*cos(alfa+k))), abs((sin(angoli(4))*ac*cos(alfa))+abs(cos(angoli(4))*ac*sin(alfa))) 0; +cos(angoli(3)+pi) +cos(angoli(1)+pi) +cos(angoli(4)+pi) 0 ; +sin(angoli(3)+pi) +sin(angoli(1)+pi) +sin(angoli(4)+pi) 1 ; (cos(angoli(3)+pi)*de*sin(angoli(2))+sin(angoli(3)+pi)*de*cos(angoli(2))), 0 (cos(angoli(4)+pi)*(de+fe)*sin(angoli(2))+sin(angoli(4)+pi)*(de+fe)*cos(angoli(2))), dk*cos(angoli(2))];
else if angoli(1)>pi/2 && angoli(1)<pi && angoli(4)>pi/2 && angoli(4)<pi %config 4 A=[ 0 abs((cos(angoli(1))*ab*sin(alfa+k))-abs(sin(angoli(1))*ab*cos(alfa+k))), abs((sin(angoli(4))*ac*cos(alfa))+abs(cos(angoli(4))*ac*sin(alfa))) 0; +cos(angoli(3)+pi) +cos(angoli(1)+pi) +cos(angoli(4)+pi) 0 ; +sin(angoli(3)+pi) +sin(angoli(1)+pi) +sin(angoli(4)+pi) 1 ; (cos(angoli(3)+pi)*de*sin(angoli(2))+sin(angoli(3)+pi)*de*cos(angoli(2))), 0 (cos(angoli(4)+pi)*(de+fe)*sin(angoli(2))+sin(angoli(4)+pi)*(de+fe)*cos(angoli(2))), dk*cos(angoli(2))];
end end end End
[L,U,P]=lu(A); %fattorizzazione LU della matrice dei coefficienti y=fwsub(L,P*b); forze=bksub(U,y); if forze(1)>0 && forze(4)>0.75 && angoli(3)>0 && forze(4)<2 && angoli(3)<pi %forza(4) è la forza di sgancio %l'IF filtra solo le forze 1 e 4 %maggiori di 0
abx=ab*cos(alfa+k); aby=ab*sin(alfa+k); bdx=bd*cos(angoli(1)); bdy=bd*sin(angoli(1)); dex=de*cos(angoli(2)); dey=de*sin(angoli(2)); ehx=eh*cos(angoli(3)); ehy=eh*sin(angoli(3)); acx=ac*cos(alfa); acy=ac*sin(alfa); cfx=cf*cos(angoli(4)); cfy=cf*sin(angoli(4)); fex=fe*cos(angoli(2)+pi); fey=fe*sin(angoli(2)+pi); x1=[0,abx,abx+bdx,abx+bdx+dex]; y1=[0,aby,aby+bdy,aby+bdy+dey]; u1=[abx,bdx,dex,ehx]; v1=[aby,bdy,dey,ehy]; x2=[0,acx,acx+cfx,acx+cfx+fex]; y2=[0,acy,acy+cfy,acy+cfy+fey]; u2=[acx,cfx,fex,ehx]; v2=[acy,cfy,fey,ehy]; figure(z) quiver(x1,y1,u1,v1,0); hold on quiver(x2,y2,u2,v2,0); z=z+1; angoli=angoli./pi.*180; AB=[AB,ab]; BD=[BD,bd]; DE=[DE,de]; EH=[EH,eh]; AC=[AC,ac]; FE=[FE,fe]; CF=[CF,cf]; ANGOLI=[ANGOLI;angoli]; %ANGOLI è una matrice n*4 dove n dipende dal numero di cicli FORZE=[FORZE,forze]; %FORZE è una matrice 4*n
end end end
end end end end end end
close(barra); %chiude la barra end toc |

|
Il parametro angolare alfa viene fornito allo script come ingresso noto, altrimenti si avrebbero più di 4 variabili che non sarebbero risolvibili con le 4 equazioni che possediamo. Questo parametro è stato fatto variare “manualmente” eseguendo più volte lo script. In seguito abbiamo introdotto un ciclo for per ogni asta che permette di variare la loro lunghezza entro un range, accuratamente selezionato tramite un’analisi preliminare 2D su Catia. Ciò permette di generare in modo automatico più di 10000 diverse geometrie. All’interno della catena di cicli for, lo script risolve il sistema di quattro equazioni scalari che si ottengono proiettando sugli assi principali le due chiusure. Il sistema in esame è non lineare e per risolverlo abbiamo utilizzato la funzione fsolve, già implementata in Matlab e che richiama un metodo numerico iterativo. A questo punto dello script, la geometria del sistema è completamente definita e tramite i valori di lunghezze e angoli calcolati abbiamo risolto il sistema di 4 equazioni in 4 incognite che riguarda l’equilibrio di forze. Questo sistema è lineare, quindi per risolverlo abbiamo utilizzato il metodo della fattorizzazione LU. Come abbiamo anticipato il sistema di equazioni riguardanti le forze cambia a seconda della posizione dei punti B e C rispetto al centro del disco. Per questo abbiamo adattato lo script scrivendone tre versioni, una per ogni famiglia di cinematismo e, all’interno di ognuna di esse, abbiamo analizzato i vari casi che si presentano a seconda dei versi delle reazioni R2 e R3. Risolto anche il sistema di forze lo script salva tutti i dati della configurazione all’interno di una matrice, in modo tale che una volta ultimata l’esecuzione, i risultati di tutte le configurazioni siano facilmente consultabili. Tenendo conto che lo script è stato eseguito più volte variando il parametro alfa, in totale, sono state analizzate circa 110 mila configurazioni differenti. Per restringere il campo di scelta sono stati inseriti dei particolari filtri all’interno dello script in modo tale che tutte le configurazioni non adeguate, siano automaticamente scartate. In particolare i filtri sono: · La somma delle lunghezze di tutte le aste deve essere maggiore della lunghezza del vettore fisso AH, altrimenti l’equazione vettoriale risulta non coerente; · Flag: visto che la funzione fsolve comporta un metodo iterativo, non vi è la certezza che giunga a convergenza per tutte le geometrie quindi, grazie alla bandierina d’uscita della funzione, riusciamo a scartare automaticamente tutte le configurazioni per le quali il metodo non è arrivato ad una soluzione precisa; · R1 > 0: in modo tale che la forza lungo l’asta HE produca un momento sulla manopola che permetta alla stessa di rimanere a battuta quando l’interruttore è chiuso; · R4 > 0,75 N: rappresenta la forza di sgancio che dobbiamo minimizzare e questo vincolo ci è stato imposto dall’azienda per questioni di stabilità e sicurezza; · R4 < 2 N: questo vincolo è stato scelto perché siamo interessati solo alle geometrie che generano una forza di sgancio che sia la più piccola possibile; · Vincoli generici sugli angoli per questioni costruttive.
Grazie a questi vincoli siamo stati in grado di limitare molto efficacemente il numero di geometrie fornite dallo script. Per facilitare la scelta finale, nell’ultima parte dello script, abbiamo implementato un codice che permette di stampare a schermo la vera e propria equazione di chiusura di ogni geometria idonea. Questo ha consentito di velocizzare molto la fase di scelta della configurazione perché si sono potuti valutare istantaneamente l’ingombro e la struttura interna dell’interruttore. Alla fine di tutta l’analisi quindi abbiamo scelto la geometria che restituiva la forza di sgancio minore tra quelle costruttivamente possibili e che risulta essere di 0,86 N. |

|
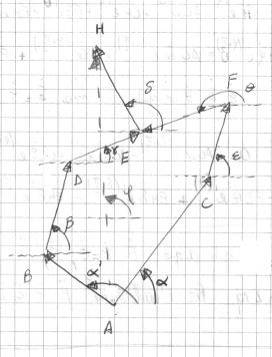
Fig. 10 Stampa a schermo di Matlab della configurazione scelta. Rappresenta la doppia equazione di chiusura |
|
Abbiamo riportato per intero il codice Matlab che ci ha permesso di effettuare una completa analisi statica. In testa allo script abbiamo assegnato i valori delle dimensioni note fissate nelle ipotesi. |